题目内容
7.2016年2月11日,美国“激光干涉引力波天文台”(LIGO)团队向全世界宣布发现了引力波,这个引力波来自于距离地球13亿光年之外一个双黑洞系统的合并.已知光在真空中传播的速度为c,太阳的质量为M0,万有引力常量为G.(1)两个黑洞的质量分别为太阳质量的26倍和39倍,合并后为太阳质量的62倍.利用所学知识,求此次合并所释放的能量.
(2)黑洞密度极大,质量极大,半径很小,以最快速度传播的光都不能逃离它的引力,因此我们无法通过光学观测直接确定黑洞的存在.假定黑洞为一个质量分布均匀的球形天体.
a.因为黑洞对其他天体具有强大的引力影响,我们可以通过其他天体的运动来推测黑洞的存在.天文学家观测到,有一质量很小的恒星独自在宇宙中做周期为T,半径为r0的匀速圆周运动.由此推测,圆周轨道的中心可能有个黑洞.利用所学知识求此黑洞的质量M;
b.严格解决黑洞问题需要利用广义相对论的知识,但早在相对论提出之前就有人利用牛顿力学体系预言过黑洞的存在.我们知道,在牛顿体系中,当两个质量分别为m1、m2的质点相距为r时也会具有势能,称之为引力势能,其大小为Ep=-G$\frac{{m}_{1}{m}_{2}}{r}$(规定无穷远处势能为零).请你利用所学知识,推测质量为M′的黑洞,之所以能够成为“黑”洞,其半径R最大不能超过多少?
分析 (1)根据爱因斯坦质能方程求出合并释放的能量.
(2)a、根据万有引力提供向心力,结合轨道半径和周期求出黑洞的质量M.
b、抓住临界状态,即黑洞第二宇宙速度等于光速,物体脱离黑洞时速度恰好为0,结合能量守恒定律求出半径R的最大值.
解答 解:(1)有题目叙述可知,两个黑洞在合并时类似于发生核聚变反应,所释放的能量来源于质量亏损,根据爱因斯坦质能方程得
$△E=△m•{c}_{\;}^{2}=(26+39-62){M}_{0}^{\;}•{c}_{\;}^{2}$=$3{M}_{0}^{\;}•{c}_{\;}^{2}$
(2)a、由题目条件可知,质量很小的恒星在其做圆周运动的轨道中心的黑洞吸引力下运动,则万有引力提供恒星运动的向心力.设恒星质量为m,则有
$G\frac{Mm}{{r}_{0}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}{r}_{0}^{\;}$
解得:$M=\frac{4{π}_{\;}^{2}{r}_{0}^{3}}{G{T}_{\;}^{2}}$
b、这里需要阅读前面关于黑洞的解释,黑洞密度大,质量极大,半径很小,以最快速度传播的光都不能逃离它的引力.物体想要逃离黑洞,至少要达到黑洞的第二宇宙速度,根据题目叙述可知,黑洞的第二宇宙速度大于等于光速,物体脱离黑洞是指在黑洞产生的引力场中到达无穷远时速度依然大于等于0.对于临界情况(黑洞第二宇宙速度等于光速,物体脱离黑洞时速度恰好为0),由能量守恒定律可知
$\frac{1}{2}m{c}_{\;}^{2}+(-G\frac{M′m}{R})=0$
解得$R=\frac{2GM′}{{c}_{\;}^{2}}$
答:(1)此合并所释放的能量$3{M}_{0}^{\;}•{c}_{\;}^{2}$
(2)a、此黑洞质量M为$\frac{4{π}_{\;}^{2}{r}_{0}^{3}}{G{T}_{\;}^{2}}$
b、黑洞半径最大不能超过$\frac{2GM}{{c}_{\;}^{2}}$
点评 该题结合黑洞的物理现象考查万有引力定律的应用,并能够与爱因斯坦质能方程相结合,有较好的创新型,是一道理论联系实际的好题.

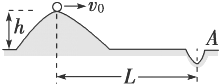 2011年8月深圳大运会高尔夫球女子团体比赛中,中华台北队获两枚金牌,中国女队队员黎佳韵在个人赛中也有不俗表现.随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图4-2-24所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )
2011年8月深圳大运会高尔夫球女子团体比赛中,中华台北队获两枚金牌,中国女队队员黎佳韵在个人赛中也有不俗表现.随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图4-2-24所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A穴所用的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2g}{h}}$ | |
| D. | 球被击出后受到的水平风力的大小为$\frac{mgh}{L}$ |
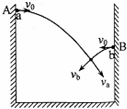 如图所示,将a、b两小球均以大小为20m/s的初速度分别从A、B两点间隔3s先后水平相向抛出,两小球恰好在空中相遇,且相遇时速度方向相互垂直,不计空气阻力,取g=10m/s2,则抛出点A、B间的水平距离是( )
如图所示,将a、b两小球均以大小为20m/s的初速度分别从A、B两点间隔3s先后水平相向抛出,两小球恰好在空中相遇,且相遇时速度方向相互垂直,不计空气阻力,取g=10m/s2,则抛出点A、B间的水平距离是( )| A. | 100m | B. | 80m | C. | 60m | D. | 约109.7m |
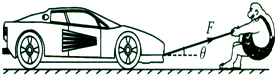 漫画中的大力士用绳子拉动汽车,绳中的拉力为F,绳与水平方向的夹角为θ.若将F沿水平和竖直方向分解,则其竖直方向的分力为( )
漫画中的大力士用绳子拉动汽车,绳中的拉力为F,绳与水平方向的夹角为θ.若将F沿水平和竖直方向分解,则其竖直方向的分力为( )| A. | Fsinθ | B. | Fcosθ | C. | $\frac{F}{sinθ}$ | D. | $\frac{F}{cosθ}$ |
| A. | 所有发射成功的卫星的速度都维持在7.9km/s | |
| B. | 所有在轨运行的卫星的速度都不会小于7.9km/s | |
| C. | 第一宇宙速度的数值是由地球的质量和半径决定的 | |
| D. | 月球绕地球运动的速度一定比7.9km/s大 |
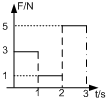
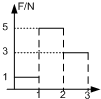
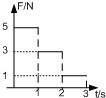




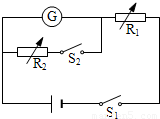 在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: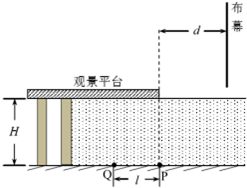 一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求: