题目内容
19.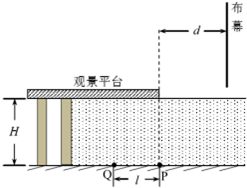 一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:Ⅰ.该光源发出的光照射到布幕上的最高点距水面的高度h;
Ⅱ.该光源发出的光能射出水面的最远位置距观景平台右侧的最远距离s.
分析 Ⅰ、射向观景台右侧边缘的光线折射后射到布幕上的位置最高,作出光路图,由数学知识求折射角的正弦值,即可由折射定律求出入射角的正弦,再由数学知识求解高度h.
Ⅱ、点光源S接近水面时,入射角为90°,光能照亮的距离最远,由折射定律求出折射角,即可由几何知识求解最远距离.
解答  解:Ⅰ、如图所示,射向观景台右侧边缘的光线折射后射到布幕上的位置最高.由折射定律得:
解:Ⅰ、如图所示,射向观景台右侧边缘的光线折射后射到布幕上的位置最高.由折射定律得:
n=$\frac{sini}{sinr}$
而sinr=$\frac{l}{\sqrt{{l}^{2}+{H}^{2}}}$
解得 sini=0.8
而 sini=$\frac{d}{\sqrt{{d}^{2}+{h}^{2}}}$
解得 h=3m
Ⅱ、点光源S接近水面时,光在观景台右侧面与水面交接处掠射到水里时,被照亮的距离为最远距离,此时,入射角为90°,折射角为临界角C.
根据sinC=$\frac{1}{n}$
以及 sinC=$\frac{s+l}{\sqrt{(s+l)^{2}+{H}^{2}}}$
解得 s=($\frac{12\sqrt{7}}{7}$-3)m
答:
Ⅰ.该光源发出的光照射到布幕上的最高点距水面的高度h是3m;
Ⅱ.该光源发出的光能射出水面的最远位置距观景平台右侧的最远距离s是($\frac{12\sqrt{7}}{7}$-3)m.
点评 本题以折射率和全反射为命题背景考查学生的推理能力和分析综合能力,关键能运用数学知识求解入射角和折射角的正弦值,知道入射角最大时折射角也最大.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
14. 过山车是一项惊险、剌激的游戏,是目前很多游乐场的必备设施.如图所示为过山车轨道的某一部分,它由两圆弧形轨道通过一直线轨道连接而成,一辆过山车正从高处圆弧沿轨道自由加速下滑,在过山车下滑到低处圆弧轨道最低点的过程中,下列说法正确的是( )
过山车是一项惊险、剌激的游戏,是目前很多游乐场的必备设施.如图所示为过山车轨道的某一部分,它由两圆弧形轨道通过一直线轨道连接而成,一辆过山车正从高处圆弧沿轨道自由加速下滑,在过山车下滑到低处圆弧轨道最低点的过程中,下列说法正确的是( )
 过山车是一项惊险、剌激的游戏,是目前很多游乐场的必备设施.如图所示为过山车轨道的某一部分,它由两圆弧形轨道通过一直线轨道连接而成,一辆过山车正从高处圆弧沿轨道自由加速下滑,在过山车下滑到低处圆弧轨道最低点的过程中,下列说法正确的是( )
过山车是一项惊险、剌激的游戏,是目前很多游乐场的必备设施.如图所示为过山车轨道的某一部分,它由两圆弧形轨道通过一直线轨道连接而成,一辆过山车正从高处圆弧沿轨道自由加速下滑,在过山车下滑到低处圆弧轨道最低点的过程中,下列说法正确的是( )| A. | 过山车一直处于失重状态 | |
| B. | 过山车在运动过程中加速度方向不变 | |
| C. | 过山车在轨道最低点时对轨道的压力大于自身重力 | |
| D. | 过山车下滑过程中减小的重力势能大于增加的动能 |
4.某质量为m的卫星绕地球做匀速圆周运动,其轨道离地面的高度等于地球的半径R,已知地球表面的重力加速度为g,忽略地球的自转效应,则( )
| A. | 卫星的绕行速度大小为$\frac{1}{2}$$\sqrt{gR}$ | |
| B. | 卫星的绕行周期大小为2π$\sqrt{\frac{2R}{g}}$ | |
| C. | 卫星所在处的重力加速度大小为$\frac{1}{2}$g | |
| D. | 卫星的动能大小为$\frac{1}{4}$mgR |
8.已知氦离子(He+)的能级图如图所示,根据能级跃迁理论可知( )


| A. | 氦离子(He+)从n=4能级跃迁到n=3能级比从n=3能级跃迁到n=2能级辐射出光子的频率低 | |
| B. | 大量处在n=3能级的氦离子(He+)向低能级跃迁,只能发出2种不同频率的光子 | |
| C. | 氦离子(He+)处于n=1能级时,能吸收45eV的能量后跃迁到n=2能级,多余的能量以光子形式放出 | |
| D. | 氦离子(He+)从n=4能级跃迁到n=3能级时辐射出的光子能使逸出功为2.55eV的金属发生光电效应 | |
| E. | 氦离子(He+)处于n=1能级时,能吸收55eV的能量 |
10.人造地球卫星在运行中,火箭沿线速度反向喷火,喷火后在新的轨道上仍能做匀速圆周运动,则( )
| A. | a减小,T增大,r减小 | B. | a减小,T减小,r减小 | ||
| C. | a减小,T增大,r增大 | D. | a增大,T减小,r增大 |
 如图所示,为一磁约束装置的原理图,同心圆内存在有垂直圆平面的匀强磁场,同心圆圆心O与xOy平面坐标系原点重合.半径为R0的圆形区域Ⅰ内有方向垂直xOy平面向里的匀强磁场B1.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(0、R0)的A点沿y轴负方向射入磁场区域Ⅰ,粒子全部经过x轴上的P点,方向沿x轴正方向.当在环形区域Ⅱ加上方向垂直于xOy平面的匀强磁场B2时,上述粒子仍从A点沿y轴负方向射入区域Ⅰ,粒子恰好能够约束在环形区域内,且经过环形区域Ⅱ后能够从Q点沿半径方向射入区域Ⅰ,已知OQ与x轴正方向成60°.不计重力和粒子间的相互作用.求:
如图所示,为一磁约束装置的原理图,同心圆内存在有垂直圆平面的匀强磁场,同心圆圆心O与xOy平面坐标系原点重合.半径为R0的圆形区域Ⅰ内有方向垂直xOy平面向里的匀强磁场B1.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(0、R0)的A点沿y轴负方向射入磁场区域Ⅰ,粒子全部经过x轴上的P点,方向沿x轴正方向.当在环形区域Ⅱ加上方向垂直于xOy平面的匀强磁场B2时,上述粒子仍从A点沿y轴负方向射入区域Ⅰ,粒子恰好能够约束在环形区域内,且经过环形区域Ⅱ后能够从Q点沿半径方向射入区域Ⅰ,已知OQ与x轴正方向成60°.不计重力和粒子间的相互作用.求: 一质量m=0.5kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图象(sin37°=0.6,cos37°=0.8,g取10m/s2).求:
一质量m=0.5kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图象(sin37°=0.6,cos37°=0.8,g取10m/s2).求: