题目内容
2.某同学用如图1所示注射器验证玻意耳定律.实验开始时在如图所示的注射器中用橡皮帽封闭了一定质量的空气.则: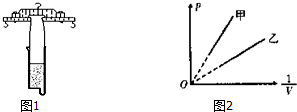
(1)若注射器上全部刻度的容积为V,用刻度尺测得全部刻度长为L,则活塞的横截面积可表示为$\frac{V}{L}$;
(2)测得活塞和框架的总质量是M,大气压强为P0,当注射器内气体处于某状态时,在框架左右两侧对称挂两个砝码,每个砝码质量为m,不计活塞与注射器管壁间摩擦,则稳定后注射器内气体的压强可表示为${P}_{0}+\frac{(M+2m)gL}{V}$;
(3)如图2中是不同小组的甲、乙两同学在同一温度下做实验时得到的P-$\frac{1}{V}$图.若两人实验时操作均正确无误,且选取坐标标度相同,那么两图线斜率不同的主要原因是研究气体质量不同.
分析 玻意耳定律研究的是一定质量理想气体的等温变化,压强与体积成反比,或压强与体积的倒数成正比,气体的体积V=SL,压强的定义式是P=$\frac{F}{S}$,结合平衡条件可解决问题.
解答 解:(1)注射器可看做圆柱体,由V=SL得:S=$\frac{V}{L}$…①
(2)装置达到稳定状态后,设气体压强为p,由平衡条件知:
p0S+(M+2m)g=pS…②
由①②可得:p=p0+$\frac{(M+2m)gL}{V}$.
(3)图线的斜率k=$\frac{P}{\frac{1}{V}}=PV$,根据克拉柏龙方程PV=nRT知,当n(指气体的物质的量)相同时,T不同,k就不同;同样,即使T相同,若n取值不同,图线斜率也不同.所以图线斜率不同的主要原因是:研究气体质量不同(或同质量气体在不同温度下研究).
故答案为:$\frac{V}{L}$,${P}_{0}+\frac{(M+2m)gL}{V}$,研究气体质量不同
点评 玻意耳定律要求气体质量恒定且温度不变,分析封闭气体压强时可采用受力平衡法.

练习册系列答案
相关题目
13. 如图所示,某游戏中有一隧道跟半径为R=125m的圆形桥在M点相接,M为桥的顶点,桥上N点与圆心O的连线跟M0的夹角为37°,与MON在同一竖直面的平台上边缘P点比M点高h=20m.当玩具小车从M越过N点后,从P点水平射出的速度多大都不能直接击中它.为了使发射的小球能击中桥上的小车,速度v0的取值范围是(不计空气阻力,sin37°=0.6,g取10m/s2)( )
如图所示,某游戏中有一隧道跟半径为R=125m的圆形桥在M点相接,M为桥的顶点,桥上N点与圆心O的连线跟M0的夹角为37°,与MON在同一竖直面的平台上边缘P点比M点高h=20m.当玩具小车从M越过N点后,从P点水平射出的速度多大都不能直接击中它.为了使发射的小球能击中桥上的小车,速度v0的取值范围是(不计空气阻力,sin37°=0.6,g取10m/s2)( )
 如图所示,某游戏中有一隧道跟半径为R=125m的圆形桥在M点相接,M为桥的顶点,桥上N点与圆心O的连线跟M0的夹角为37°,与MON在同一竖直面的平台上边缘P点比M点高h=20m.当玩具小车从M越过N点后,从P点水平射出的速度多大都不能直接击中它.为了使发射的小球能击中桥上的小车,速度v0的取值范围是(不计空气阻力,sin37°=0.6,g取10m/s2)( )
如图所示,某游戏中有一隧道跟半径为R=125m的圆形桥在M点相接,M为桥的顶点,桥上N点与圆心O的连线跟M0的夹角为37°,与MON在同一竖直面的平台上边缘P点比M点高h=20m.当玩具小车从M越过N点后,从P点水平射出的速度多大都不能直接击中它.为了使发射的小球能击中桥上的小车,速度v0的取值范围是(不计空气阻力,sin37°=0.6,g取10m/s2)( )| A. | v0<30m/s | B. | v0>40m/s | ||
| C. | 22.5m/s≤v0≤40m/s | D. | 22.5m/s≤v0≤30m/s |
10.如图甲为一种改进后的回旋加速器示意图,其中盒缝间的加速电场场强大小恒定,且被限制在AC板间,虚线中间不需加电场,如图所示,从P0处静止释放一带电粒子,粒子将沿电场线方向加速后再进入D形盒中的匀强磁场做匀速圆周运动,对这种改进后的回旋加速器,工作时某带电粒子的动能Ek随时间t变化规律如图乙所示(忽略带电粒子在电场中的加速时间),则下列判断正确的是( )

| A. | 所加电场方向需要做周期性的变化,且变化周期等子2(tn-tn-1) | |
| B. | 粒子在磁场中做圆周运动的周期为tn-tn-1 | |
| C. | 不同粒子在同一回旋加速器中获得的最大动能都相同 | |
| D. | 带电粒子每运动一周被加速一次 |
17.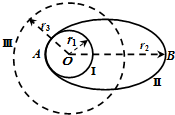 地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )
地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )
 地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )
地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )| A. | 卫星在近地圆轨道Ⅰ上运行的周期与地球自转周期相同 | |
| B. | 从轨道Ⅰ发射到轨道Ⅱ需要在近地的A点一次性给它提供能量$\frac{GMm}{4R}$ | |
| C. | 卫星在椭圆轨道上的周期为T0$\sqrt{(\frac{{r}_{2}+R}{R})^{3}}$ | |
| D. | 卫星在椭圆轨道Ⅱ上自由运行时,它在B点的机械能大于在A点的机械能 |
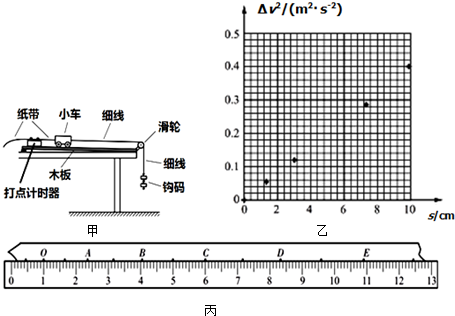
11.某实验小组采用如图甲所示的装置研究“小车运动变化规律”.打点计时器工作频率为50Hz.实验的部分步骤如下:
a.将木板的左端垫起,以平衡小车的摩擦力;
b.在小车中放入砝码,带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
c.将小车停在打点计时器附近,接通电源,释放小车,小车拖动纸带,打点计时器在纸带上打下一系列的点,断开电源;
d.改变钩码或小车中砝码的质量,更换纸带,重复b、c的操作.
(1)设钩码质量为m1、砝码和小车总质量为m2,重力加速度为g,则小车的加速度为:a=$\frac{{m}_{1}g}{{m}_{1}+{m}_{2}}$(用题中所给字母表示);
(2)如图丙是某次实验中得到的一条纸带,在纸带上取计数点O、A、B、C、D和E,用最小刻度是毫米的刻度尺进行测量,读出各计数点对应的刻度x,通过计算得到各计数点到O的距离s以及对应时刻小车的瞬时速度v.请将C点对应的测量xC值和计算速度vC值填在下表中的相应位置.
(3)实验小组通过绘制△v2-s图线来分析运动规律(其中△v2=v2-v02,v是各计数点对应时刻小车的瞬时速度,v0是O点对应时刻小车的瞬时速度).他们根据实验数据在图乙中标出了O、A、B、D、E对应的坐标点,请你图乙中标出计数点C对应的坐标点,并画出△v2-s图线.
(4)实验小组绘制的△v2-s图线的斜率k=$\frac{2{m}_{1}g}{{m}_{1}+{m}_{2}}$(用题中所给字母表示),若发现该斜率大于理论值,其原因可能是木板的左侧垫的过高.

a.将木板的左端垫起,以平衡小车的摩擦力;
b.在小车中放入砝码,带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
c.将小车停在打点计时器附近,接通电源,释放小车,小车拖动纸带,打点计时器在纸带上打下一系列的点,断开电源;
d.改变钩码或小车中砝码的质量,更换纸带,重复b、c的操作.
(1)设钩码质量为m1、砝码和小车总质量为m2,重力加速度为g,则小车的加速度为:a=$\frac{{m}_{1}g}{{m}_{1}+{m}_{2}}$(用题中所给字母表示);
(2)如图丙是某次实验中得到的一条纸带,在纸带上取计数点O、A、B、C、D和E,用最小刻度是毫米的刻度尺进行测量,读出各计数点对应的刻度x,通过计算得到各计数点到O的距离s以及对应时刻小车的瞬时速度v.请将C点对应的测量xC值和计算速度vC值填在下表中的相应位置.
(3)实验小组通过绘制△v2-s图线来分析运动规律(其中△v2=v2-v02,v是各计数点对应时刻小车的瞬时速度,v0是O点对应时刻小车的瞬时速度).他们根据实验数据在图乙中标出了O、A、B、D、E对应的坐标点,请你图乙中标出计数点C对应的坐标点,并画出△v2-s图线.
(4)实验小组绘制的△v2-s图线的斜率k=$\frac{2{m}_{1}g}{{m}_{1}+{m}_{2}}$(用题中所给字母表示),若发现该斜率大于理论值,其原因可能是木板的左侧垫的过高.
| 计数点 | x/cm | s/cm | v/(m•s-1) |
| O | 1.00 | 0.30 | |
| A | 2.34 | 1.34 | 0.38 |
| B | 4.04 | 3.04 | 0.46 |
| C | 6.00 | 5.00 | 0.54 |
| D | 8.33 | 7.33 | 0.61 |
| E | 10.90 | 9.90 | 0.70 |
12. 如图所示,相距为L的点电荷A、B带电量分别为+4Q和-Q.今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )
如图所示,相距为L的点电荷A、B带电量分别为+4Q和-Q.今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )
 如图所示,相距为L的点电荷A、B带电量分别为+4Q和-Q.今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )
如图所示,相距为L的点电荷A、B带电量分别为+4Q和-Q.今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )| A. | -Q,在A左侧距A为L处 | B. | -2Q,在A左侧距A为$\frac{L}{2}$处 | ||
| C. | +2Q,在B右侧距B 为$\frac{3L}{2}$处 | D. | +4Q,在B右侧距B为L处 |
 如图所示,有一四棱镜ABCD,∠B=∠C=90°,∠D=75°.某同学想测量其折射率,他用激光笔从BC面上的P点射入一束激光,从Q点射出时与AD面的夹角为30°,Q点到BC面垂线的垂足为E,P、Q两点到E点的距离分别为a、$\sqrt{3}$a,已知真空中光束为c,求:
如图所示,有一四棱镜ABCD,∠B=∠C=90°,∠D=75°.某同学想测量其折射率,他用激光笔从BC面上的P点射入一束激光,从Q点射出时与AD面的夹角为30°,Q点到BC面垂线的垂足为E,P、Q两点到E点的距离分别为a、$\sqrt{3}$a,已知真空中光束为c,求: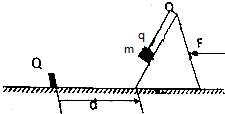 如图所示,在粗糙水平面上有一质量为M=2kg的粗糙斜面体、斜面的倾角θ=30°,在斜面体的左侧相距为d=1.5m处有一固定障碍物Q,将一质量为m=0.2kg的小物块(可视为质点)用绝缘绳系住,绳的一端固定在斜面体的顶端,此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力.现给斜面体施加一水平向左的推力F,使斜面体和小物块一起向左做匀加速运动,当斜面体到达障碍物Q与其碰撞后,斜面体立即被障碍物Q锁定.已知斜面体与地面间的动摩擦因数为μ1=0.5,重力加速度g=10m/s2,设滑动摩擦力等于最大静摩擦力,求:
如图所示,在粗糙水平面上有一质量为M=2kg的粗糙斜面体、斜面的倾角θ=30°,在斜面体的左侧相距为d=1.5m处有一固定障碍物Q,将一质量为m=0.2kg的小物块(可视为质点)用绝缘绳系住,绳的一端固定在斜面体的顶端,此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力.现给斜面体施加一水平向左的推力F,使斜面体和小物块一起向左做匀加速运动,当斜面体到达障碍物Q与其碰撞后,斜面体立即被障碍物Q锁定.已知斜面体与地面间的动摩擦因数为μ1=0.5,重力加速度g=10m/s2,设滑动摩擦力等于最大静摩擦力,求: