题目内容
13.一导热气缸竖直地放在水平地面上,开口向上.现将一活塞K放入气缸,给K以适当的力,使K缓缓下移至距气缸上端$\frac{1}{3}$缸长时撤去力,K恰好可静止于此处(在此过程中温度不变).这时再轻轻盖上一个与K质量相等的铝盖P,P与缸上端接触良好,此时K上下的温度都是27℃.现对缸内气体缓慢加热,当K向上移动至距缸顶$\frac{1}{6}$缸长时达到平衡,求此时缸内的温度.分析 气体等温压缩,根据平衡条件求解出初、末状态的气压,然后根据玻意耳定律列式求解;在活塞上放上P后,由理想气体的状态方程即可解答.
解答 解:设气缸长L,缸内气体先发生等温变化,缓慢下移至距气缸上端$\frac{L}{3}$时,撤去力,活塞恰好静止,活塞受力平衡有${p}_{0}^{\;}S+mg=pS$①
初态:${p}_{1}^{\;}={p}_{0}^{\;}$ ${V}_{1}^{\;}=LS$
末态:${p}_{2}^{\;}={p}_{\;}^{\;}$ ${V}_{2}^{\;}=\frac{2}{3}LS$
根据玻意耳定律有${p}_{0}^{\;}LS=({p}_{0}^{\;}+\frac{mg}{S})\frac{2}{3}LS$
解得$\frac{1}{2}$${p}_{0}^{\;}S=mg$
放上质量相等的铝盖后,对活塞和铝盖整体有${p}_{0}^{\;}S+2mg={p}_{3}^{\;}S$
解得:${p}_{3}^{\;}=2{p}_{0}^{\;}$
设活塞K上移至$\frac{L}{6}$时,设温度为${T}_{3}^{\;}$.,${V}_{3}^{\;}=\frac{5}{6}LS$
根据理想气体状态方程有$\frac{{p}_{0}^{\;}LS}{300}=\frac{2{p}_{0}^{\;}\frac{5}{6}LS}{{T}_{3}^{\;}}$
解得${T}_{3}^{\;}=500K$,即${t}_{3}^{\;}=227℃$
答:对缸内气体缓慢加热,当K向上移动至距缸顶$\frac{1}{6}$缸长时达到平衡,此时缸内的温度227℃
点评 本题关键是通过对活塞受力分析通过力平衡法求气体压强,分析清楚气体状态变化过程,应用玻意耳定律、理想气体状态方程即可正确解题.

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案| A. | 内、外电阻相差1Ω | B. | 内、外电阻之和为1Ω | ||
| C. | 外电阻为1Ω | D. | 内电阻为1Ω |
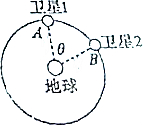 2015年3月30日,我国成功发射一颗北斗导航卫星.这是我国发射的第17颗北斗导航卫星,这次成功发射,标志着北斗导航系统由区域运行开始向全球组网.如图所示,北斗导航系统中的两颗地球同步卫星1、2轨道半径均为r,某时刻分别位于轨道上的A、B两个位置,若卫星均沿顺时针方向运行,地球表面的重力加速为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )
2015年3月30日,我国成功发射一颗北斗导航卫星.这是我国发射的第17颗北斗导航卫星,这次成功发射,标志着北斗导航系统由区域运行开始向全球组网.如图所示,北斗导航系统中的两颗地球同步卫星1、2轨道半径均为r,某时刻分别位于轨道上的A、B两个位置,若卫星均沿顺时针方向运行,地球表面的重力加速为g,地球半径为R,不计卫星间的相互作用力,下列判断正确的是( )| A. | 卫星1向后喷气就一定能够追上卫星2 | |
| B. | 两卫星及其各部分均处于完全失重状态 | |
| C. | 这两颗卫星的线速度大小相等,均为$\sqrt{\frac{GM}{r}}$ | |
| D. | 卫星1由A位置石动到B位置所需的时间是$\frac{θ}{R}$$\sqrt{\frac{{r}^{3}}{g}}$ |
 一物体静止在水平地面上,现给物体施加一竖直向上的拉力作用,不计空气阻力,物体机械能E与物体升高的高度h之间的关系图象如图所示,其中图线在A点处的切线的斜率最大,在B点处的切线水平,h2~h3的图线为平行于横轴的直线,则下列说法正确的是( )
一物体静止在水平地面上,现给物体施加一竖直向上的拉力作用,不计空气阻力,物体机械能E与物体升高的高度h之间的关系图象如图所示,其中图线在A点处的切线的斜率最大,在B点处的切线水平,h2~h3的图线为平行于横轴的直线,则下列说法正确的是( )| A. | h2~h3过程中拉力的功率为零 | |
| B. | 0~h2过程中物体所受拉力始终大于重力 | |
| C. | 在h2处物体的速度最大 | |
| D. | 在h1处物体所受的拉力最大 |

 质谱仪是一种精密仪器,是测量带电粒子的质量和分析同位素的重要工具,从粒子源S产生粒子束(初速度可视为零),经电势差为U的加速电场加速后,垂直进入磁感应强度为B的匀强磁场,粒子束中一个电荷量为+q的粒子经匀强磁场,最终垂直打在记录它照相底片上的P点,测得P点到粒子进入磁场处的距离为l,粒子所受重力不计,求:
质谱仪是一种精密仪器,是测量带电粒子的质量和分析同位素的重要工具,从粒子源S产生粒子束(初速度可视为零),经电势差为U的加速电场加速后,垂直进入磁感应强度为B的匀强磁场,粒子束中一个电荷量为+q的粒子经匀强磁场,最终垂直打在记录它照相底片上的P点,测得P点到粒子进入磁场处的距离为l,粒子所受重力不计,求: