题目内容
12. 如图所示,相距为L的点电荷A、B带电量分别为+4Q和-Q.今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )
如图所示,相距为L的点电荷A、B带电量分别为+4Q和-Q.今引入第三个点电荷C,使三个点电荷都处于平衡状态,则C的电量和放置的位置是( )| A. | -Q,在A左侧距A为L处 | B. | -2Q,在A左侧距A为$\frac{L}{2}$处 | ||
| C. | +2Q,在B右侧距B 为$\frac{3L}{2}$处 | D. | +4Q,在B右侧距B为L处 |
分析 A、B、C三个点电荷都处于静止状态,对电荷受力分析,每个电荷都处于受力平衡状态,故根据库仑定律可分别对任意两球进行分析列出平衡方程即可求得结果.
解答 解:引入的电荷C要处于平衡状态,电荷C所在位置的场强就要为零,A、B两电荷产生电场的合场强为零处在A、B两电荷的外侧,且离电荷量大的点电荷远,由此可知,点电荷C应放在点电荷B的外侧.如图所示,电荷C所在位置处A、B两电荷产生电场的合场强为零,即A、B两电荷在C处产生电场的大小相等,有
k$\frac{4Q}{{{{(L+x)}^2}}}$=k$\frac{Q}{x^2}$
同理,电荷B所在位置,点电荷A、C的产生的电场的场强在B处大小也应相等,
又有:k$\frac{4Q}{L^2}$=k$\frac{Q_c}{x^2}$
解上两式即可得C电荷应放在B点电荷的外侧,距B点电荷x=L处,C电荷的电荷量QC=4Q.
故选:D.
点评 此题是利用合电场的场强为零来判断电荷系统的平衡问题,当研究的电场在产生电场的两点电荷的连线上时,有关场强在同一直线上,可以用代数方法运算.

练习册系列答案
相关题目
3.下列说法正确的是( )
| A. | 安培发现了电流磁效应;法拉第发现了电磁感应现象 | |
| B. | 开普勒首先发现了行星运动规律;哈雷利用万有引力定律推算出彗星的回归周期 | |
| C. | 库伦发现了点电荷的相互规律并提出了电场线;密立根通过油滴实验测定了元电荷的数值 | |
| D. | 富兰克林首先命名了正负电荷;奥斯特通过实验发现在磁场中转动的金属圆盘可以对外输出电流 |
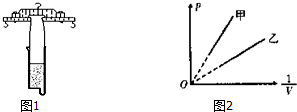
7. 如图所示,气垫导轨的滑块上安装了宽度为d的遮光板,做加速运动的滑块先后通过两个光电门,数字毫秒计记录了遮光板通过第一个光电门的时间为t1,通过第二个光电门的时间为t2,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t,下列测量结果中最接近真实值的是( )
如图所示,气垫导轨的滑块上安装了宽度为d的遮光板,做加速运动的滑块先后通过两个光电门,数字毫秒计记录了遮光板通过第一个光电门的时间为t1,通过第二个光电门的时间为t2,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t,下列测量结果中最接近真实值的是( )
 如图所示,气垫导轨的滑块上安装了宽度为d的遮光板,做加速运动的滑块先后通过两个光电门,数字毫秒计记录了遮光板通过第一个光电门的时间为t1,通过第二个光电门的时间为t2,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t,下列测量结果中最接近真实值的是( )
如图所示,气垫导轨的滑块上安装了宽度为d的遮光板,做加速运动的滑块先后通过两个光电门,数字毫秒计记录了遮光板通过第一个光电门的时间为t1,通过第二个光电门的时间为t2,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为△t,下列测量结果中最接近真实值的是( )| A. | 滑块运动的加速度为$\frac{{d({t_1}-{t_2})}}{{{t_1}{t_2}(△t)}}$ | |
| B. | 滑块运动的加速度为$\frac{{2d({t_1}-{t_2})}}{{{t_1}{t_2}[{2(△t)+{t_2}-{t_1}}]}}$ | |
| C. | 遮光板中点通过第一个光电门的速度为$\frac{d}{t_1}$ | |
| D. | 遮光板前沿通过第一个光电门的速度为$\frac{d}{t_1}$ |
17.关于热现象,下列说法正确的是( )
| A. | 物体的动能和重力势能也是其内能的一部分 | |
| B. | 悬浮在液体中的颗粒越小,温度越高,布朗运动越剧烈 | |
| C. | 液晶与多晶体一样具有各向同性 | |
| D. | 当分子间的引力与斥力平衡时,分子势能最小 | |
| E. | 若一定质量的理想气体在膨胀的同时放出热量,则气体分子的平均动能减小 |
4.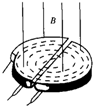 回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
 回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )| A. | 带电粒子从D形盒射出时的动能与加速电压无关 | |
| B. | 带电粒子从D形盒射出时的动能与磁场的强弱有关 | |
| C. | 带电粒子做一次圆周运动,要被加速两次,因此交变电场的周期应为圆周运动周期的二倍 | |
| D. | 用同一回旋加速器分别加速不同的带电粒子,不用调节交变电场的频率 |
1.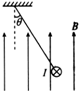 一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )
一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )
 一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )
一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )| A. | 磁场未转动时,绝缘细线对通电导线的拉力大小为2.5N | |
| B. | 该磁场的磁感应强度大小为1.5T | |
| C. | 转动过程中绝缘细线与竖直方向的夹角先变大后变小 | |
| D. | 转动过程中绝缘细线受到的拉力最小值为1.6N |
 如图所示,粗细均匀的L形细玻璃管AOB,OA、OB两部分长度均为20cm,OA部分水平、右端开口,管内充满水银,OB部分竖直、上端封闭.现将玻璃管在竖直平面内绕O点逆时针方向缓慢旋转53°,此时被封闭气体长度为x.缓慢加热管内封闭气体至温度T,使管内水银恰好不溢出管口.已知大气压强为75cmHg,室温为27℃,sin53°=0.8,$\sqrt{12369}≈111$.
如图所示,粗细均匀的L形细玻璃管AOB,OA、OB两部分长度均为20cm,OA部分水平、右端开口,管内充满水银,OB部分竖直、上端封闭.现将玻璃管在竖直平面内绕O点逆时针方向缓慢旋转53°,此时被封闭气体长度为x.缓慢加热管内封闭气体至温度T,使管内水银恰好不溢出管口.已知大气压强为75cmHg,室温为27℃,sin53°=0.8,$\sqrt{12369}≈111$.