题目内容
14.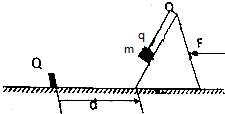 如图所示,在粗糙水平面上有一质量为M=2kg的粗糙斜面体、斜面的倾角θ=30°,在斜面体的左侧相距为d=1.5m处有一固定障碍物Q,将一质量为m=0.2kg的小物块(可视为质点)用绝缘绳系住,绳的一端固定在斜面体的顶端,此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力.现给斜面体施加一水平向左的推力F,使斜面体和小物块一起向左做匀加速运动,当斜面体到达障碍物Q与其碰撞后,斜面体立即被障碍物Q锁定.已知斜面体与地面间的动摩擦因数为μ1=0.5,重力加速度g=10m/s2,设滑动摩擦力等于最大静摩擦力,求:
如图所示,在粗糙水平面上有一质量为M=2kg的粗糙斜面体、斜面的倾角θ=30°,在斜面体的左侧相距为d=1.5m处有一固定障碍物Q,将一质量为m=0.2kg的小物块(可视为质点)用绝缘绳系住,绳的一端固定在斜面体的顶端,此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力.现给斜面体施加一水平向左的推力F,使斜面体和小物块一起向左做匀加速运动,当斜面体到达障碍物Q与其碰撞后,斜面体立即被障碍物Q锁定.已知斜面体与地面间的动摩擦因数为μ1=0.5,重力加速度g=10m/s2,设滑动摩擦力等于最大静摩擦力,求:(1)小物块与斜面间的动摩擦因数μ2;
(2)最大的水平推力F;
(3)若用最大水平推力作用在斜面体上,斜面体被障碍物Q锁定后,小物体在绝缘绳牵引下沿圆周运动而不脱离圆轨道,轻绳的长度应满足的条件?
分析 (1)抓住物块恰好能够静止在斜面上,根据共点力平衡条件求出小物块与斜面间的动摩擦因数μ2.
(2)当物块所受的静摩擦力沿斜面向下达到最大时,加速度最大,水平推力即最大.隔离对物块分析,求出物块的最大加速度,再对整体分析,根据牛顿第二定律求出水平推力F的大小.
(3)根据速度位移公式求出物块抛出的初速度,结合圆周运动最高点的临界条件和机械能守恒定律求解.
解答 解:(1)物块恰好静止在斜面上且绳刚好伸直无弹力,则有:
mgsinθ=μ2mgcosθ
解得:μ2=tanθ=$\frac{\sqrt{3}}{3}$
(2)当物块所受的静摩擦力沿斜面向下达到最大时,需要加速度最大,对物块受力分析,由牛顿第二定律可得:
竖直方向有 FNcosθ=mg+fmsinθ…①
水平方向有 FNsinθ+fmcosθ=mam…②
fm=μ2FN…③
由以上三式可解得:am=$\sqrt{3}$g
对整体列式:F-μ1(M+m)g=(M+m)am
解得:F=(M+m)(gμ1+am)=(11+2$\sqrt{3}$)N
(3)物块抛出的速度为:v0=$\sqrt{2{a}_{m}d}$=2$\sqrt{5\sqrt{3}}$m/s2.
设轻绳的长度为L.
在圆周的最高点有 m$\frac{{v}^{2}}{L}$≥mg
从抛出到最高点,由机械能守恒定律有
mgL(1+sinθ)+$\frac{1}{2}$mv2=$\frac{1}{2}m{v}_{0}^{2}$
联立解得 L≤$\frac{\sqrt{3}}{2}$m
答:
(1)小物块与斜面间的动摩擦因数μ2是$\frac{\sqrt{3}}{3}$.
(2)最大的水平推力F是(11+2$\sqrt{3}$)N.
(3)轻绳的长度应满足的条件是L≤$\frac{\sqrt{3}}{2}$m.
点评 本题考查了牛顿第二定律和运动学公式的综合,得出物块最大加速度是解决本题的关键,掌握整体法和隔离法在动力学中的运用.

| A. | 5 6 | B. | 8 4 | C. | 8 6 | D. | 6 6 |
| A. | 安培发现了电流磁效应;法拉第发现了电磁感应现象 | |
| B. | 开普勒首先发现了行星运动规律;哈雷利用万有引力定律推算出彗星的回归周期 | |
| C. | 库伦发现了点电荷的相互规律并提出了电场线;密立根通过油滴实验测定了元电荷的数值 | |
| D. | 富兰克林首先命名了正负电荷;奥斯特通过实验发现在磁场中转动的金属圆盘可以对外输出电流 |
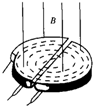 回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )| A. | 带电粒子从D形盒射出时的动能与加速电压无关 | |
| B. | 带电粒子从D形盒射出时的动能与磁场的强弱有关 | |
| C. | 带电粒子做一次圆周运动,要被加速两次,因此交变电场的周期应为圆周运动周期的二倍 | |
| D. | 用同一回旋加速器分别加速不同的带电粒子,不用调节交变电场的频率 |
 质谱仪是一种精密仪器,是测量带电粒子的质量和分析同位素的重要工具,从粒子源S产生粒子束(初速度可视为零),经电势差为U的加速电场加速后,垂直进入磁感应强度为B的匀强磁场,粒子束中一个电荷量为+q的粒子经匀强磁场,最终垂直打在记录它照相底片上的P点,测得P点到粒子进入磁场处的距离为l,粒子所受重力不计,求:
质谱仪是一种精密仪器,是测量带电粒子的质量和分析同位素的重要工具,从粒子源S产生粒子束(初速度可视为零),经电势差为U的加速电场加速后,垂直进入磁感应强度为B的匀强磁场,粒子束中一个电荷量为+q的粒子经匀强磁场,最终垂直打在记录它照相底片上的P点,测得P点到粒子进入磁场处的距离为l,粒子所受重力不计,求: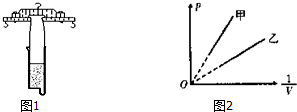
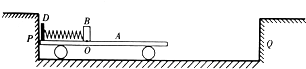

 如图所示,某同学为验证动能定理设计了如图所示的实验,橡皮筋固定在桌子的右端,一质量为m的小车固定在橡皮筋上,小车在O位置时橡皮筋恰好处于原长,完全相同的橡皮筋条数可以更换,A位置为光电门,小车上挡板的宽度为D,OA间的距离为L,砝码与托盘的总质量为M,小车与桌面间的摩擦忽略不计.
如图所示,某同学为验证动能定理设计了如图所示的实验,橡皮筋固定在桌子的右端,一质量为m的小车固定在橡皮筋上,小车在O位置时橡皮筋恰好处于原长,完全相同的橡皮筋条数可以更换,A位置为光电门,小车上挡板的宽度为D,OA间的距离为L,砝码与托盘的总质量为M,小车与桌面间的摩擦忽略不计.