题目内容
8. 如图所示,足够长的平行金属导轨MN、M′N′处于方向水平向左、磁感应强度B1=$\frac{5}{6}T$的匀强磁场中,两导轨间的距离L=1m,导轨右端N、N′连接着与水平面成θ=30°的足够长光滑平行导轨NO、N′O′、NN′垂直于MN,倾斜导轨处于方向垂直与导轨向上、磁感应轻度B2=1T的匀强磁场中,两根金属杆P、Q的质量均为m=1kg,电阻均为R=0.5Ω,杆与水平导轨间的动摩擦因数为μ=0.4,现将P杆放置与NN′处并给其平行于水平导轨向左v=5m/s的初速度,与此同时,使Q杆在一平行导轨向下的外力F的作用下,从静止开始做加速度为a=6m/s2的匀加速运动,Q杆距离NN′足够远,Q杆一直在斜轨上运动,不考虑感应电流产生磁场的影响,导轨电阻不计,g取10m/s2
如图所示,足够长的平行金属导轨MN、M′N′处于方向水平向左、磁感应强度B1=$\frac{5}{6}T$的匀强磁场中,两导轨间的距离L=1m,导轨右端N、N′连接着与水平面成θ=30°的足够长光滑平行导轨NO、N′O′、NN′垂直于MN,倾斜导轨处于方向垂直与导轨向上、磁感应轻度B2=1T的匀强磁场中,两根金属杆P、Q的质量均为m=1kg,电阻均为R=0.5Ω,杆与水平导轨间的动摩擦因数为μ=0.4,现将P杆放置与NN′处并给其平行于水平导轨向左v=5m/s的初速度,与此同时,使Q杆在一平行导轨向下的外力F的作用下,从静止开始做加速度为a=6m/s2的匀加速运动,Q杆距离NN′足够远,Q杆一直在斜轨上运动,不考虑感应电流产生磁场的影响,导轨电阻不计,g取10m/s2(1)求Q杆下滑过程中,外力F与时间t的函数关系;
(2)求P杆停止时Q杆已运动的位移S;
(3)已知P杆进入水平轨道直到停止的过程中,外力F对Q杆所做的功为15J,求这一过程中系统产生的总热量Q总.
分析 (1)Q杆下滑时做匀加速运动,根据牛顿第二定律和安培力与速度的关系式,得到F和t的关系.
(2)Q杆在斜轨道滑行中,P杆在水面上作减速运动,对P杆,根据牛顿第二定律列式,得到加速度与时间的关系,由P杆的加速度与时间的图象可知:图象与时间轴所围成的面积表示P杆速度的变化量,即M杆停止时,速度的改变量大小,列式求出M杆运动时间,根据两杆运动的同时性,得到Q杆的运动时间,再由位移时间公式求解Q杆运动的位移s.
(3)这一过程中系统产生的总热量等于P杆摩擦产生的热量和Q杆产生的焦耳热之和.根据功能关系分别求解得出
解答 解:(1)Q杆在斜轨道滑行过程中,设受到的安培力为F安,由左手定则可判断安培力沿斜面向上
沿着斜面方向有:F+mgsin30°-F安=ma
F安=B2IL I=$\frac{{B}_{2}Lv}{2R}$
Q杆匀加速运动 v=at
将m=1kg B2=1T L=1m R=0.5Ω a=6m/s2
代入得:F+1×10×$\frac{1}{2}$-1×$\frac{1×1×6t}{2×0.5}$×1=1×a
化简整理得:F=1+6t
(2)Q杆在斜轨道滑行时,P杆在水平面上做减速运动,设P杆受到的安培力为F安,由左手定则可判断安培力水平向右
对P杆受力分析结合牛顿第二定律得:f=μN=μ(mg+F安)
F安=B1IL I=$\frac{{B}_{2}Lv}{2R}$
Q杆匀加速运动 v=at
对P受力分析结合牛顿第二定律可得:
f=ma
将m=1kg B2=1T L=1m R=0.5Ω a=6m/s2
代入得:0.4×(1×10+$\frac{5}{6}$×$\frac{1×1×6t}{2×0.5}$×1)=1×a
得:a=4+2t
P杆作加速度逐渐增大的减速运动,在P杆加速度与时间的图象中,可知围成的面积是P杆速度的变化量
当P杆停止时,速度的改变量大小为5m/s.
设P杆经过时间t恰好停止运动.速度的变化量△vP=5m/s△vP=$\frac{1}{2}$(4+4+2t)
解得:t=1s
对Q杆:s=$\frac{1}{2}$at2=$\frac{1}{2}$×6×1=3m
(3)设摩擦力对P杆做的功为Wf、安培力做功为W安
对于P杆根据动能定理:Wf=0$-\frac{1}{2}m{v}^{2}$
Wf=0$-\frac{1}{2}$×1×52=12.5J
对于Q杆根据动能定理:W安+WF+(mgsinθ)s=$\frac{1}{2}$mv2
v=at
代入数据得:W安+15J+(1×10×$\frac{1}{2}$)×3=$\frac{1}{2}$×1(6×1)2
W安=-12J
所以两金属棒共同产生的焦耳热 Q焦=W克安=12J
总热量 Q总=W克f+W克安=12.5J+12J=24.5J
答(1)求Q杆下滑过程中,外力F与时间t的函数关系为F=1+6t
(2)求P杆停止时Q杆已运动的位移S=3m;
(3)已知P杆进入水平轨道直到停止的过程中,外力F对Q杆所做的功为15J,求这一过程中系统产生的总热量Q总=24.5J
点评 本题是复杂的电磁感应问题,离不开力和运动关系的分析、功和能关系的分析.对于热量,若回路中电流是变化的,往往根据能量守恒定律求解

| A. | 实验使用的两细绳必须等长 | |
| B. | 每次将橡皮条沿相同方向拉到相同长度 | |
| C. | 弹黉秤、细绳、橡皮条都应与木板平行 | |
| D. | 用两弹簧秤同时拉细绳时两弹簧秤拉力夹角越大越好 | |
| E. | 拉橡皮条的细绳要适当长些,标记同一细绳方向的两点要稍远些 |
 将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并排放在一起,现用水平力F垂直于B的左边推B物体,使A、B整体仍保持矩形沿F方向匀速运动,则( )
将某均匀的长方体锯成如图所示的A、B两块后,放在水平桌面上并排放在一起,现用水平力F垂直于B的左边推B物体,使A、B整体仍保持矩形沿F方向匀速运动,则( )| A. | 物体A在水平方向上受三个力的作用,且合力为零 | |
| B. | 物体A在水平方向上受两个力的作用,且合力为零 | |
| C. | B对A的压力等于桌面对A的摩擦力 | |
| D. | B对A的作用力方向与F方向相同 |
 两个完全相同的条形磁铁放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁均处于水平位置上,且静止不动.
两个完全相同的条形磁铁放在平板AB上,磁铁的N、S极如图所示.开始时平板及磁铁均处于水平位置上,且静止不动.(1)现将AB突然竖直向上平移(平板与磁铁之间始终接触),并使之停在A′B′处,结果发现两个条形磁铁吸在了一起.
(2)如果将AB从原来位置突然竖直向下平移,并使之停在A″B″处,结果发现两条磁铁也吸在了一起.则下列说法正确的是( )
| A. | 开始时两磁铁静止不动,说明磁铁间的作用力是排斥力 | |
| B. | 开始时两磁铁静止不动,说明磁铁间的吸引力小于静摩擦力 | |
| C. | 第(1)过程中磁铁开始滑动时,平板正在向上加速 | |
| D. | 第(2)过程中磁铁开始滑动时,平板正在向下加速 |
 如图所示,滑块A和B用轻细绳连接在一起后放在水平桌面上,水平恒力F作用在B上,使A,B一起由静止开始沿水平桌面滑动.已知滑块A、B与水平桌面件的动摩擦因数为μ,力F作用时间t后,A,B件连线断开,此后力F仍作用于B,试求:滑块A刚刚停住时,滑块B的速度为多大?设滑块A,B的质量分别为mA,mB.
如图所示,滑块A和B用轻细绳连接在一起后放在水平桌面上,水平恒力F作用在B上,使A,B一起由静止开始沿水平桌面滑动.已知滑块A、B与水平桌面件的动摩擦因数为μ,力F作用时间t后,A,B件连线断开,此后力F仍作用于B,试求:滑块A刚刚停住时,滑块B的速度为多大?设滑块A,B的质量分别为mA,mB.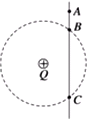 如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时的速度大小为$\sqrt{7gh}$.求:
如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时的速度大小为$\sqrt{7gh}$.求:
 如图所示,斜面AB倾角为30°,底端A点与斜面上B点相距10m,甲、乙两物体大小不计,与斜面间的动摩擦因数为$\frac{\sqrt{3}}{2}$,某时刻甲从A点沿斜面以v1=10m/s的初速度滑向B,同时乙物体从B点以v2=7.25m/s的初速度滑向A,(g=10m/s2 最大静摩擦力等于滑动摩擦力)求:
如图所示,斜面AB倾角为30°,底端A点与斜面上B点相距10m,甲、乙两物体大小不计,与斜面间的动摩擦因数为$\frac{\sqrt{3}}{2}$,某时刻甲从A点沿斜面以v1=10m/s的初速度滑向B,同时乙物体从B点以v2=7.25m/s的初速度滑向A,(g=10m/s2 最大静摩擦力等于滑动摩擦力)求: