题目内容
17.如图甲所示,水平传送带的长度L=6m,传送带皮带轮的半径都为R=0.25m,现有一小物体(可视为质点)以一定的水平速度v0滑上传送带,设皮带轮顺时针匀速转动,当角速度为ω时,物体离开传送带B端后在空中运动的水平距离为s,若皮带轮以不同的角速度重复上述动作(保持滑上传送带的初速v0不变),可得到一些对应的ω和s值,将这些对应值画在坐标上并连接起来,得到如图乙中实线所示的 s-ω图象,根据图中标出的数据(g取10m/s2 ),求: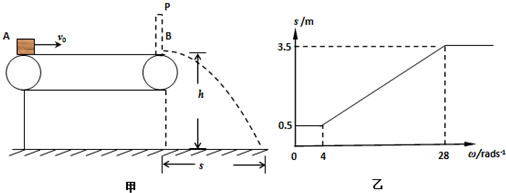
(1)B端距地面的高度h
(2)滑上传送带时的初速v0以及物体和皮带间的动摩擦因数μ
(3)若在B端加一竖直挡板P,皮带轮以角速度ω′=16rad/s顺时针匀速转动,物体与挡板连续两次碰撞的时间间隔t′为多少?(物体滑上A端时速度仍为v0,在和挡板碰撞中无机械能损失)
分析 (1)从图象中知,当ω=4rad/s时,物块匀减速运动到达B点的速度正好等于皮带的速度,根据水平位移求出时间,再根据时间求出高度.
(2)从图象中知,当0≤ω≤4rad/s时,物块的速度大于皮带的速度,物体一直做匀减速运动.有2μgL=v02-v12.当ω≥28rad/s时,水平位移不变,知物块一直做匀加速运动.有2μgL=v22-v02.分别求出v2,v1,联立两方程求出v0和μ.
(3)由v′=ω′R求出传送带的速度.物体与挡板碰撞后向左减速至零,再向右加速,由牛顿第二定律和速度公式结合求解.
解答 解:(1)由图乙可知,当皮带轮以角速度ω1=4rad/s时,
物体离开皮带做平抛运动的初速度为:v1=ω1 R=4×0.25m/s=1m/s
水平距离为s=0.5m,有:t=$\frac{s}{{v}_{1}^{\;}}$=$\frac{0.5}{1}s$=0.5s
h=$\frac{1}{2}g{t^2}$=$\frac{1}{2}×10×0.{5}_{\;}^{2}$=1.25m
(2)由图象可知:当ω≤ω1=4rad/s时,物体在传送带上一直减速,
由牛顿第二定律得,加速度大小为a=μg
到达B点时的速度为v1,有:v02-v12=2μgL
代入数据:${v}_{0}^{2}-{1}_{\;}^{2}=2μ×60$…①
当ω≥28rad/s时,物体在传送带上一直加速,
经过B点时的速度为:v2=ω2 R=7m/s,
有:v22-v02=2μgL
代入数据:${7}_{\;}^{2}-{v}_{0}^{2}=2μ×60$…②
联立①②解得:μ=0.2 v0=5m/s
(3)当ω′=16rad/s时,皮带速度为:v′=ω′R=16×0.25m/s=4m/s
物体以v0=5m/s的速度开始减速,有:s′=$\frac{{(v_0^2-{v^{'2}})}}{2a}$=$\frac{{5}_{\;}^{2}-{4}_{\;}^{2}}{2×2}$=2.25m<L
故物体碰到挡板前已经减速到v′=4m/s,
由题意知物体和板碰撞前后的速度大小都是v′=4m/s
由运动的对称性得:t'=2 $\frac{v′}{a}$=$2×\frac{4}{2}$s=4s
答:(1)小物体的初速度v0为5m/s,它与传送带间的动摩擦因数μ为0.2.
(2)B端距地面高度h为1.25m.
(3)物体与挡板连续两次碰撞的时间间隔是4s.
点评 解决本题的关键理清物块在传送带上运动的可能性,抓住临界状态,结合运动学公式进行分析.

 一学生去实验室取定值电阻两只,R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如图,电源输出电压U=12.0V不变.该生先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )
一学生去实验室取定值电阻两只,R1=10Ω,R2=30Ω,电压表一个,练习使用电压表测电压.电路连接如图,电源输出电压U=12.0V不变.该生先用电压表与R1并联,电压表示数为U1,再用电压表与R2并联,电压表示数为U2,则下列说法正确的是( )| A. | U2一定小于9.0v | B. | U1一定大于3.0 V | ||
| C. | U1与U2之和小于12 V | D. | U1与U2之比一定不等于1:3 |
 2016年暑假,小明到黄山旅游,乘观光车看西海大峡谷.如图所示,假设该缆车沿着某段坡度为30°的滑道以加速度a=1m/s2保持竖直状态上行,在缆车中与滑道平行的斜面上放一个相对斜面静止的质量为m=1kg的物块,g取10m/s2,则( )
2016年暑假,小明到黄山旅游,乘观光车看西海大峡谷.如图所示,假设该缆车沿着某段坡度为30°的滑道以加速度a=1m/s2保持竖直状态上行,在缆车中与滑道平行的斜面上放一个相对斜面静止的质量为m=1kg的物块,g取10m/s2,则( )| A. | 物块受到的摩擦力方向平行斜面向下 | |
| B. | 物块受到的摩擦力大小为6N | |
| C. | 物块受到的摩擦力大小为1N | |
| D. | 物块受到斜面的弹力大小为5N |
 如图所示,质量分别为m和2m所小球A和B,用轻弹簧相连后再用细线悬挂于电梯内,已知电梯正在竖直向上做匀加速直线运动,细线上的拉力为F.此时突然剪断细线,在细线断的瞬间,弹簧的弹力大小和小球A的加速度大小分别为( )
如图所示,质量分别为m和2m所小球A和B,用轻弹簧相连后再用细线悬挂于电梯内,已知电梯正在竖直向上做匀加速直线运动,细线上的拉力为F.此时突然剪断细线,在细线断的瞬间,弹簧的弹力大小和小球A的加速度大小分别为( )| A. | $\frac{F}{3}$,$\frac{F}{3m}$+g | B. | $\frac{F}{3}$,$\frac{2F}{3m}$+g | C. | $\frac{2F}{3}$,$\frac{F}{3m}$+g | D. | $\frac{2F}{3}$,$\frac{2F}{3m}$+g |
 如图所示,足够长的平行金属导轨MN、M′N′处于方向水平向左、磁感应强度B1=$\frac{5}{6}T$的匀强磁场中,两导轨间的距离L=1m,导轨右端N、N′连接着与水平面成θ=30°的足够长光滑平行导轨NO、N′O′、NN′垂直于MN,倾斜导轨处于方向垂直与导轨向上、磁感应轻度B2=1T的匀强磁场中,两根金属杆P、Q的质量均为m=1kg,电阻均为R=0.5Ω,杆与水平导轨间的动摩擦因数为μ=0.4,现将P杆放置与NN′处并给其平行于水平导轨向左v=5m/s的初速度,与此同时,使Q杆在一平行导轨向下的外力F的作用下,从静止开始做加速度为a=6m/s2的匀加速运动,Q杆距离NN′足够远,Q杆一直在斜轨上运动,不考虑感应电流产生磁场的影响,导轨电阻不计,g取10m/s2
如图所示,足够长的平行金属导轨MN、M′N′处于方向水平向左、磁感应强度B1=$\frac{5}{6}T$的匀强磁场中,两导轨间的距离L=1m,导轨右端N、N′连接着与水平面成θ=30°的足够长光滑平行导轨NO、N′O′、NN′垂直于MN,倾斜导轨处于方向垂直与导轨向上、磁感应轻度B2=1T的匀强磁场中,两根金属杆P、Q的质量均为m=1kg,电阻均为R=0.5Ω,杆与水平导轨间的动摩擦因数为μ=0.4,现将P杆放置与NN′处并给其平行于水平导轨向左v=5m/s的初速度,与此同时,使Q杆在一平行导轨向下的外力F的作用下,从静止开始做加速度为a=6m/s2的匀加速运动,Q杆距离NN′足够远,Q杆一直在斜轨上运动,不考虑感应电流产生磁场的影响,导轨电阻不计,g取10m/s2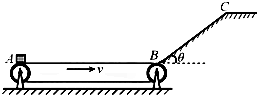 用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:
用如图所示的浅色水平传送带AB和斜面BC将货物运送到斜面的顶端.AB距离L=11m,传送带始终以v=12m/s匀速顺时针运行.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔t=1.0s将一个质量m=10kg、底部有碳粉的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的$\frac{1}{11}$,不计传送带轮的大小,g=10m/s2(sin37°=0.6,cos37°=0.8).求:
 超市一送水员用双轮小车运送桶装矿泉水.装运完毕,如图所示,在拉运过程中保持图示角度不变,不计桶与小车之间摩擦力的影响.求:(g=10m/s2)
超市一送水员用双轮小车运送桶装矿泉水.装运完毕,如图所示,在拉运过程中保持图示角度不变,不计桶与小车之间摩擦力的影响.求:(g=10m/s2)