题目内容
3. 如图所示,A、B两小球用等长的绝缘细线悬挂,它们所带电荷量分别为QA=2×10-8C,QB=-2×10-8 C,A、B相距 3cm.在水平方向的外界匀强电场作用下A、B保持静止,悬线都沿竖直方向.由此可知外电场的场强大小是2×105N/C,方向水平向左,A、B中点处的合电场的场强大小是1.4×106N/C,方向水平向右.
如图所示,A、B两小球用等长的绝缘细线悬挂,它们所带电荷量分别为QA=2×10-8C,QB=-2×10-8 C,A、B相距 3cm.在水平方向的外界匀强电场作用下A、B保持静止,悬线都沿竖直方向.由此可知外电场的场强大小是2×105N/C,方向水平向左,A、B中点处的合电场的场强大小是1.4×106N/C,方向水平向右.
分析 A球带正电,B球带负电,B对A的吸引力水平向右,要使A处于竖直方向平衡,就要加一个水平向左的电场,使A受到的电场力等于B球对A的吸引力.由平衡条件求解.再根据电场的叠加原理求两球的中点处的总电场强度.
解答 解:由题意可知A球受力平衡,水平方向合外力等于零,B对A的作用力向右,所以要加一个水平向左的电场,且以A为研究对象,有:
QAE=k$\frac{{Q}_{A}{Q}_{B}}{{r}^{2}}$
得:E=k$\frac{{Q}_{B}}{{r}^{2}}$=9×109×$\frac{2×1{0}^{-8}}{0.0{3}^{2}}$=2×105N/C
A、B两质点连线中点处的场强是两个点电荷与匀强电场的矢量和,两个点电荷的方向都向右,E方向向左,所以:E′=2•k$\frac{{Q}_{A}}{(\frac{r}{2})^{2}}$-E=7E=1.4×106N/C,方向水平向右.
故答案为:2×105N/C,水平向左,1.4×106N/C,水平向右.
点评 本题主要考查了库仑定律及电荷在电场中要受到力的作用,根据小球受力平衡求解,能熟练运用电场的叠加原理求合场强.

练习册系列答案
相关题目
14. 如图1所示,光滑平行竖直金属导轨AB、CD相距L,在A、C之间接一个阻值为R的电阻,在两导轨间abcd矩形区域内有垂直导轨平面竖直向上、磁感应强度大小为B、宽为5d的匀强磁场.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合),现用一个竖直向上的力F拉导体棒,使它由静止开始运动,已知导体棒离开磁场前已开始做匀速直线运动,导体棒与导轨始终垂直且保持良好接触,导轨电阻不计,F随导体棒与初始位置的距离x变化的情况如图2所示,重力加速度为g,下列判断正确的是( )
如图1所示,光滑平行竖直金属导轨AB、CD相距L,在A、C之间接一个阻值为R的电阻,在两导轨间abcd矩形区域内有垂直导轨平面竖直向上、磁感应强度大小为B、宽为5d的匀强磁场.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合),现用一个竖直向上的力F拉导体棒,使它由静止开始运动,已知导体棒离开磁场前已开始做匀速直线运动,导体棒与导轨始终垂直且保持良好接触,导轨电阻不计,F随导体棒与初始位置的距离x变化的情况如图2所示,重力加速度为g,下列判断正确的是( )
 如图1所示,光滑平行竖直金属导轨AB、CD相距L,在A、C之间接一个阻值为R的电阻,在两导轨间abcd矩形区域内有垂直导轨平面竖直向上、磁感应强度大小为B、宽为5d的匀强磁场.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合),现用一个竖直向上的力F拉导体棒,使它由静止开始运动,已知导体棒离开磁场前已开始做匀速直线运动,导体棒与导轨始终垂直且保持良好接触,导轨电阻不计,F随导体棒与初始位置的距离x变化的情况如图2所示,重力加速度为g,下列判断正确的是( )
如图1所示,光滑平行竖直金属导轨AB、CD相距L,在A、C之间接一个阻值为R的电阻,在两导轨间abcd矩形区域内有垂直导轨平面竖直向上、磁感应强度大小为B、宽为5d的匀强磁场.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合),现用一个竖直向上的力F拉导体棒,使它由静止开始运动,已知导体棒离开磁场前已开始做匀速直线运动,导体棒与导轨始终垂直且保持良好接触,导轨电阻不计,F随导体棒与初始位置的距离x变化的情况如图2所示,重力加速度为g,下列判断正确的是( )| A. | 导体棒离开磁场时速度大小为$\frac{2mg(R+r)}{{B}^{2}{L}^{2}}$ | |
| B. | 导体棒经过磁场的过程中,通过电阻R的电荷量为$\frac{5BLd}{R}$ | |
| C. | 离开磁场时导体棒两端电压为$\frac{2mgR}{BL}$ | |
| D. | 导体棒经过磁场的过程中,电阻R产生焦耳热为$\frac{9mgdR{B}^{4}{L}^{4}-2{m}^{3}{g}^{2}R(R+r)^{2}}{{B}^{4}{L}^{4}(R+r)}$ |
11. 如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )
如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )
 如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )
如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )| A. | 剪断绳子的瞬间,物体A的加速度为2g | |
| B. | 弹簧恢复原长时,物体A的速度最大 | |
| C. | 弹簧压缩到最短时,物体A的加速度为零 | |
| D. | 剪断绳子后,物体A速度为零时,地面对B的力最大 |
8. 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )| A. | 编号为①的粒子在磁场区域内运动的时间为$\frac{πm}{qB}$ | |
| B. | 编号为②的粒子在磁场区域内运动的时间为$\frac{πm}{qB}$ | |
| C. | 三个粒子进入磁场的速度依次增加 | |
| D. | 三个粒子在磁场内运动的时间依次增加 |
12. 图中虚线PQ上方有一磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外.O是PQ上一点,在纸面内从O点向磁场区域的任意方向连续发射速率为v0的粒子,粒子电荷量为q、重力为m.现有两个粒子先后射入磁场中并恰好在M点相遇,MO与PQ间夹角为60°,不计粒子重力及粒子间的相互作用,则下列说法正确的是( )
图中虚线PQ上方有一磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外.O是PQ上一点,在纸面内从O点向磁场区域的任意方向连续发射速率为v0的粒子,粒子电荷量为q、重力为m.现有两个粒子先后射入磁场中并恰好在M点相遇,MO与PQ间夹角为60°,不计粒子重力及粒子间的相互作用,则下列说法正确的是( )
 图中虚线PQ上方有一磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外.O是PQ上一点,在纸面内从O点向磁场区域的任意方向连续发射速率为v0的粒子,粒子电荷量为q、重力为m.现有两个粒子先后射入磁场中并恰好在M点相遇,MO与PQ间夹角为60°,不计粒子重力及粒子间的相互作用,则下列说法正确的是( )
图中虚线PQ上方有一磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外.O是PQ上一点,在纸面内从O点向磁场区域的任意方向连续发射速率为v0的粒子,粒子电荷量为q、重力为m.现有两个粒子先后射入磁场中并恰好在M点相遇,MO与PQ间夹角为60°,不计粒子重力及粒子间的相互作用,则下列说法正确的是( )| A. | 两个粒子从O点射入磁场的时间间隔可能为$\frac{2πm}{3qB}$ | |
| B. | 两个粒子射入磁场的方向分别与PQ成30°和60°角 | |
| C. | 在磁场中运动的粒子离边界的最大距离为$\frac{2m{v}_{0}}{qB}$ | |
| D. | 垂直PQ射入磁场中的粒子在磁场中的运动时间最长 |
13.如图所示,是电源在闭合电路中的 U-I 图象,则下列正说法正确的是( )

| A. | 电源的电动势为 2.0V | B. | 电源的内阻为 4Ω | ||
| C. | 电流为 0.5A 时的外电阻是 0 | D. | 电源的短路电流为 0.5A |
 如图所示,一辆汽车上装着一个高h、宽b的匀质木箱,汽车突然以加速度a刹车,问a不能大于多少,才能确保木箱不翻到?(木箱在A点被顶住,不能向前滑动)
如图所示,一辆汽车上装着一个高h、宽b的匀质木箱,汽车突然以加速度a刹车,问a不能大于多少,才能确保木箱不翻到?(木箱在A点被顶住,不能向前滑动)
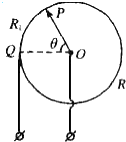 将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.
将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.