题目内容
15.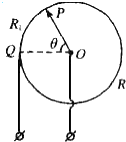 将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.
将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.
分析 圆形滑动变阻器Q、P之间的电阻为两段圆弧的电阻R1、R2并联所得的总电阻,根据$\frac{1}{R}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}$,找出总电阻与θ关系即可求解.
解答 解:圆形滑动变阻器Q、P之间的电阻为两段圆弧的电阻R1、R2并联所得的总电阻,并联电阻为:
R并=$\frac{{(\frac{θ}{2π}×16)×(\frac{2π-θ}{2π}×16)}}{{(\frac{θ}{2π}×16)+(\frac{2π-θ}{2π}×16)}}$=$\frac{{(\frac{θ}{2π}×16)×(\frac{2π-θ}{2π}×16)}}{16}$;
当R并=4Ω,解得θ=π;
当R并=3Ω,解得θ=$\frac{π}{2}$或$\frac{3}{2}π$.
故答案为:π,$\frac{π}{2}$或$\frac{3}{2}π$.
点评 本题关键是明确电路结构,为两段电阻丝并联,写出并联电阻的表达式,然后代入数据求解,基础题目.

练习册系列答案
相关题目
5. 被弯成正弦函数图象形状的导体棒a和直导体棒b放置在如图所示的坐标系中,a、b的右端通过导线与阻值R=5Ω的电阻连接,导体棒c与y轴重合,整个装置处在方向垂直坐标系向里、磁感应强度B=1T的匀强磁场中(图中未画出),除R外不计一切电阻.现使导体棒c在水平力F作用下从图示位置以v=5m/s的速度匀速运动至a、b右端,整个过程中导体棒a、b和c保持良好接触,不计一切摩擦.则( )
被弯成正弦函数图象形状的导体棒a和直导体棒b放置在如图所示的坐标系中,a、b的右端通过导线与阻值R=5Ω的电阻连接,导体棒c与y轴重合,整个装置处在方向垂直坐标系向里、磁感应强度B=1T的匀强磁场中(图中未画出),除R外不计一切电阻.现使导体棒c在水平力F作用下从图示位置以v=5m/s的速度匀速运动至a、b右端,整个过程中导体棒a、b和c保持良好接触,不计一切摩擦.则( )
 被弯成正弦函数图象形状的导体棒a和直导体棒b放置在如图所示的坐标系中,a、b的右端通过导线与阻值R=5Ω的电阻连接,导体棒c与y轴重合,整个装置处在方向垂直坐标系向里、磁感应强度B=1T的匀强磁场中(图中未画出),除R外不计一切电阻.现使导体棒c在水平力F作用下从图示位置以v=5m/s的速度匀速运动至a、b右端,整个过程中导体棒a、b和c保持良好接触,不计一切摩擦.则( )
被弯成正弦函数图象形状的导体棒a和直导体棒b放置在如图所示的坐标系中,a、b的右端通过导线与阻值R=5Ω的电阻连接,导体棒c与y轴重合,整个装置处在方向垂直坐标系向里、磁感应强度B=1T的匀强磁场中(图中未画出),除R外不计一切电阻.现使导体棒c在水平力F作用下从图示位置以v=5m/s的速度匀速运动至a、b右端,整个过程中导体棒a、b和c保持良好接触,不计一切摩擦.则( )| A. | 流过电阻R的电流方向如图中箭头所示 | |
| B. | 水平力F的最小值为0.32N | |
| C. | 水平力F的最大功率为7.2W | |
| D. | 电阻R产生的总热量为2.56J |
7. 如图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,下列说法中正确的是( )
如图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,下列说法中正确的是( )
 如图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,下列说法中正确的是( )
如图所示,A板发出的电子经加速后,水平射入水平放置的两平行金属板间,金属板间所加的电压为U,电子最终打在荧光屏P上,关于电子的运动,下列说法中正确的是( )| A. | 滑动触头向右移动时,电子打在荧光屏上的位置上升 | |
| B. | 滑动触头向左移动时,电子打在荧光屏上的位置上升 | |
| C. | 电压U增大时,电子打在荧光屏上的速度大小不变 | |
| D. | 电压U增大时,电子从发出到打在荧光屏上的时间不变 |
4. 如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )
如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )
 如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )
如图所示,已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后,水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知),小球在此空间的竖直面内做匀速圆周运动,则( )| A. | 小球可能带正电 | |
| B. | 小球做匀速圆周运动的周期为T=$\frac{2π}{Bg}$ | |
| C. | 小球做匀速圆周运动的半径为r=$\frac{1}{B}$$\sqrt{\frac{2UE}{g}}$ | |
| D. | 若电压U增大,则小球做匀速圆周运动的周期增加 |
5.在2014年仁川亚运会上,张雨涵在女子400米自由泳比赛中以4分07秒67的成绩获得冠军.张雨涵能够取得冠军,取决于她在比赛中( )
| A. | 某时刻的瞬时速度大 | B. | 触壁时的瞬时速度大 | ||
| C. | 平均速率大 | D. | 任何时刻的速度都大 |
 如图所示,水平虚线MN下方有一竖直向上的匀强电场,一根轻质绝缘杆(质量不计)两端分别套有A、B两个小球,A球的质量为m,带正电,在匀强电场中受到的电场力为其重力大小的3倍,A球和杆间的滑动摩擦力的大小等于其重力大小.B球的质量为3m,不带电,B球和杆间的滑动摩擦力大小也等于其重力大小,设两球的最大静摩擦力均等于滑动摩擦力,重力加速度为g.开始时A、B球和杆均静止,A球距MN高度为h,同时释放A、B两球和杆,当A球第二次进入电场区域时,A、B两球恰好相遇,运动过程中杆始终保持竖直状态.求:
如图所示,水平虚线MN下方有一竖直向上的匀强电场,一根轻质绝缘杆(质量不计)两端分别套有A、B两个小球,A球的质量为m,带正电,在匀强电场中受到的电场力为其重力大小的3倍,A球和杆间的滑动摩擦力的大小等于其重力大小.B球的质量为3m,不带电,B球和杆间的滑动摩擦力大小也等于其重力大小,设两球的最大静摩擦力均等于滑动摩擦力,重力加速度为g.开始时A、B球和杆均静止,A球距MN高度为h,同时释放A、B两球和杆,当A球第二次进入电场区域时,A、B两球恰好相遇,运动过程中杆始终保持竖直状态.求: 如图所示,A、B两小球用等长的绝缘细线悬挂,它们所带电荷量分别为QA=2×10-8C,QB=-2×10-8 C,A、B相距 3cm.在水平方向的外界匀强电场作用下A、B保持静止,悬线都沿竖直方向.由此可知外电场的场强大小是2×105N/C,方向水平向左,A、B中点处的合电场的场强大小是1.4×106N/C,方向水平向右.
如图所示,A、B两小球用等长的绝缘细线悬挂,它们所带电荷量分别为QA=2×10-8C,QB=-2×10-8 C,A、B相距 3cm.在水平方向的外界匀强电场作用下A、B保持静止,悬线都沿竖直方向.由此可知外电场的场强大小是2×105N/C,方向水平向左,A、B中点处的合电场的场强大小是1.4×106N/C,方向水平向右. 如图所示,空间存在着范围足够大、水平向左的匀强电场,在竖直虚线PM的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B=$\frac{m}{q}\sqrt{\frac{g}{2R}}$.一绝缘U形弯杆由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环在磁场边界左侧,P、M点在磁场边界线上,A点为圆弧上的一点,NMAP段是光滑的.现有一质量为m、带电荷量为+q的小环套在半圆环上,恰好在A点保持静止,半径OA与虚线所成夹角为θ=37°.现将带电小环由P点无初速度释放(sin37°=0.6,cos37°=0.8).求:
如图所示,空间存在着范围足够大、水平向左的匀强电场,在竖直虚线PM的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B=$\frac{m}{q}\sqrt{\frac{g}{2R}}$.一绝缘U形弯杆由两段直杆和一半径为R的半圆环组成,固定在纸面所在的竖直平面内.PQ、MN水平且足够长,半圆环在磁场边界左侧,P、M点在磁场边界线上,A点为圆弧上的一点,NMAP段是光滑的.现有一质量为m、带电荷量为+q的小环套在半圆环上,恰好在A点保持静止,半径OA与虚线所成夹角为θ=37°.现将带电小环由P点无初速度释放(sin37°=0.6,cos37°=0.8).求: