题目内容
13.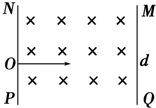 如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长也为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).
如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长也为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).
分析 粒子进入磁场中.由洛伦兹力提供向心力,由牛顿第二定律得到半径公式r=$\frac{mv}{Bq}$,粒子的速度v越大,轨迹半径r越大.粒子从ab边射出磁场时,从a点射出,轨迹半径最小,对应的速度最小,从b点射出,轨迹半径最大,对应的速度最大,根据几何关系求出半径,再由牛顿第二定律求出对应的速度,即可得到速度的范围.
解答 解:第一种极端情况从M点射出,此时轨道的圆心为O′点,由平面几何知识可得:R2=d2+(R-$\frac{1}{2}$d)2 
解得:R=$\frac{5}{4}$d.
而带电粒子在磁场中的轨道半径R,又为R=$\frac{m{v}_{0}}{{B}_{1}q}$,
所以有:B1=$\frac{4m{v}_{0}}{5qd}$=$\frac{4m{v}_{0}}{5de}$.
第二种极端情况是粒子从N点射出,此时粒子正好运动了半个圆,
其轨道半径为:R′=$\frac{1}{4}$d.
所以$\frac{1}{4}$d=$\frac{m{v}_{0}}{{B}_{2}q}$,
B2=$\frac{4m{v}_{0}}{de}$.
综合上述两种情况,得:$\frac{4m{v}_{0}}{5de}$≤B≤$\frac{4m{v}_{0}}{de}$.
答:磁感应强度B的大小范围$\frac{4m{v}_{0}}{5de}$≤B≤$\frac{4m{v}_{0}}{de}$.
点评 本题关键是由几何知识确定出从两端射出时临界情况下的半径,然后根据牛顿第二定律列方程求解即可.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
8.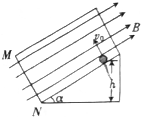 绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
 绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )
绝缘光滑斜面与水平面成α角,质量为m、带电荷量为-q(q>0)的小球从斜面上的h高度处释放,初速度为v0(v0>0),方向与斜面底边MN平行,如图所示,整个装置处在匀强磁场B中,磁场方向平行斜面向上.如果斜面足够大,且小球能够沿斜面到达底边MN.则下列判断正确的是( )| A. | 匀强磁场磁感应强度的取值范围为0≤B≤$\frac{mg}{q{v}_{0}}$ | |
| B. | 匀强磁场磁感应强度的取值范围为0≤B≤$\frac{mgcosα}{q{v}_{0}}$ | |
| C. | 小球在斜面做变加速曲线运动 | |
| D. | 小球到达底边MN的时间t=$\sqrt{\frac{2h}{gsi{n}^{2}α}}$ |
5. 如图,正方形容器处在匀强磁场中,一束电子从孔a垂直于磁场沿ab方向射入容器中,其中一部分从c孔射出,一部分从d孔射出,容器处在真空中,下列说法正确的是( )
如图,正方形容器处在匀强磁场中,一束电子从孔a垂直于磁场沿ab方向射入容器中,其中一部分从c孔射出,一部分从d孔射出,容器处在真空中,下列说法正确的是( )
 如图,正方形容器处在匀强磁场中,一束电子从孔a垂直于磁场沿ab方向射入容器中,其中一部分从c孔射出,一部分从d孔射出,容器处在真空中,下列说法正确的是( )
如图,正方形容器处在匀强磁场中,一束电子从孔a垂直于磁场沿ab方向射入容器中,其中一部分从c孔射出,一部分从d孔射出,容器处在真空中,下列说法正确的是( )| A. | 从两孔射出的电子速率之比为vc:vd=2:1 | |
| B. | 从两孔射出的电子在容器中运动的时间之比tc:td=1:2 | |
| C. | 从两孔射出的电子的加速度大小之比ac:ad=$\sqrt{2}$:1 | |
| D. | 从两孔射出的电子的加速度大小之比ac:ad=2:1 |
 如图,竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R=2Ω的电阻,N板上有一小孔Q,在金属板M、N之间CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T.有一质量M=0.2kg、电阻r=1Ω的金属棒搭在M、N之间并与M、N良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点由静止释放一个比荷$\frac{q}{m}$=1×104 C/kg的正离子,经电场加速后,以v=200m/s的速度从Q点垂直于N板边界射入右侧区域.不计离子重力,忽略电流产生的磁场,取g=10m/s2.求:
如图,竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R=2Ω的电阻,N板上有一小孔Q,在金属板M、N之间CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T.有一质量M=0.2kg、电阻r=1Ω的金属棒搭在M、N之间并与M、N良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点由静止释放一个比荷$\frac{q}{m}$=1×104 C/kg的正离子,经电场加速后,以v=200m/s的速度从Q点垂直于N板边界射入右侧区域.不计离子重力,忽略电流产生的磁场,取g=10m/s2.求: 固定在匀强磁场中的正方形导线框abcd,各边长为L,其中ab是一段电阻为R的均匀电阻丝,其余三边均为电阻可以忽略的铜线,磁感应强度为B的匀强磁场方向垂直纸面向里.现有一段与ab材料、粗细、长度均相同的电阻丝PQ架在导线框上,如图所示.若PQ以恒定速度v从ad滑向bc,当其滑过$\frac{L}{3}$的距离时,通过Pb段的电流多大?方向如何?
固定在匀强磁场中的正方形导线框abcd,各边长为L,其中ab是一段电阻为R的均匀电阻丝,其余三边均为电阻可以忽略的铜线,磁感应强度为B的匀强磁场方向垂直纸面向里.现有一段与ab材料、粗细、长度均相同的电阻丝PQ架在导线框上,如图所示.若PQ以恒定速度v从ad滑向bc,当其滑过$\frac{L}{3}$的距离时,通过Pb段的电流多大?方向如何?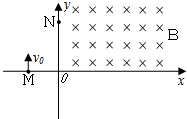 如图,在xoy平面内,第一象限内存在着方向垂直于xoy平面向里的匀强磁场,第二象限内存在着平行于x轴的匀强电场(图中未画出),一质量为m,电荷量为-q的粒子(不计重力),从直角坐标系x轴上的M点以v0的速度平行于y轴正方向射出,M点距坐标原点的距离为d,带电粒子经电场偏转后从y轴上N点进入第一象限,N点距坐标原点的距离为2d,带电粒子通过第一象限的磁场后,垂直于x轴进入第四象限.求:
如图,在xoy平面内,第一象限内存在着方向垂直于xoy平面向里的匀强磁场,第二象限内存在着平行于x轴的匀强电场(图中未画出),一质量为m,电荷量为-q的粒子(不计重力),从直角坐标系x轴上的M点以v0的速度平行于y轴正方向射出,M点距坐标原点的距离为d,带电粒子经电场偏转后从y轴上N点进入第一象限,N点距坐标原点的距离为2d,带电粒子通过第一象限的磁场后,垂直于x轴进入第四象限.求: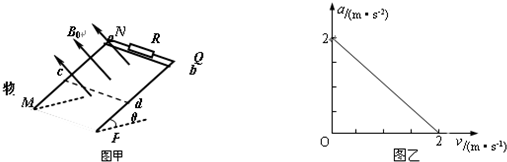
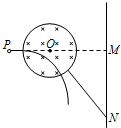 如图在P点有一电子发射源,静止的电子经一电压加速后,垂直击中屏幕上的M点,若在PM之间有一半径为R的圆形区域,该区域内存在着磁感强度为B的匀强磁场,且圆心O在PM的连线上,电子将击中屏幕的N点,已知电子电量为e,质量为m,O点与M点的距离为L,N点与M点的距离为$\sqrt{3}L$,求加速电压U为多大?
如图在P点有一电子发射源,静止的电子经一电压加速后,垂直击中屏幕上的M点,若在PM之间有一半径为R的圆形区域,该区域内存在着磁感强度为B的匀强磁场,且圆心O在PM的连线上,电子将击中屏幕的N点,已知电子电量为e,质量为m,O点与M点的距离为L,N点与M点的距离为$\sqrt{3}L$,求加速电压U为多大?