题目内容
2.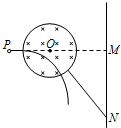 如图在P点有一电子发射源,静止的电子经一电压加速后,垂直击中屏幕上的M点,若在PM之间有一半径为R的圆形区域,该区域内存在着磁感强度为B的匀强磁场,且圆心O在PM的连线上,电子将击中屏幕的N点,已知电子电量为e,质量为m,O点与M点的距离为L,N点与M点的距离为$\sqrt{3}L$,求加速电压U为多大?
如图在P点有一电子发射源,静止的电子经一电压加速后,垂直击中屏幕上的M点,若在PM之间有一半径为R的圆形区域,该区域内存在着磁感强度为B的匀强磁场,且圆心O在PM的连线上,电子将击中屏幕的N点,已知电子电量为e,质量为m,O点与M点的距离为L,N点与M点的距离为$\sqrt{3}L$,求加速电压U为多大?
分析 画出粒子运动轨迹,根据几何关系求解半径,根据洛伦兹力提供向心力求解速度大小,再根据动能定理求解加速电压.
解答 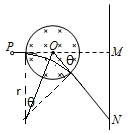 解:粒子在磁场中运动轨迹如图所示,根据图中几何关系可得:$tanθ=\frac{MN}{OM}=\frac{\sqrt{3}L}{L}=\sqrt{3}$,
解:粒子在磁场中运动轨迹如图所示,根据图中几何关系可得:$tanθ=\frac{MN}{OM}=\frac{\sqrt{3}L}{L}=\sqrt{3}$,
则有:θ=60°;
设粒子运动半径为r,则有:$tan30°=\frac{R}{r}$,
解得:r=$\sqrt{3}$R;
根据洛伦兹力提供向心力可得:evB=m$\frac{{v}^{2}}{r}$,
解得:v=$\frac{\sqrt{3}eBR}{m}$;
根据动能定理可得:eU=$\frac{1}{2}m{v}^{2}$,
解得:$U=\frac{{3e{B^2}{R^2}}}{2m}$.
答:加速电压U为$\frac{3e{B}^{2}{R}^{2}}{2m}$.
点评 对于带电粒子在磁场中的运动情况分析,一般是确定圆心位置,根据几何关系求半径,结合洛伦兹力提供向心力求解未知量;根据周期公式结合轨迹对应的圆心角求时间;带电粒子在电场中加速时可以利用动能定理来分析.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
17. 匀强磁场分布在直角三角形ACD区域内,磁感应强度大小为B,方向垂直于纸面向外,AD边长为2L,θ=30°,质量为m,电荷量为+q的粒子束以不同速度从AD边的中点P垂直AD边沿纸面射入磁场,速率最大的粒子恰好垂直CD边穿出,不考虑粒子的重力,则( )
匀强磁场分布在直角三角形ACD区域内,磁感应强度大小为B,方向垂直于纸面向外,AD边长为2L,θ=30°,质量为m,电荷量为+q的粒子束以不同速度从AD边的中点P垂直AD边沿纸面射入磁场,速率最大的粒子恰好垂直CD边穿出,不考虑粒子的重力,则( )
 匀强磁场分布在直角三角形ACD区域内,磁感应强度大小为B,方向垂直于纸面向外,AD边长为2L,θ=30°,质量为m,电荷量为+q的粒子束以不同速度从AD边的中点P垂直AD边沿纸面射入磁场,速率最大的粒子恰好垂直CD边穿出,不考虑粒子的重力,则( )
匀强磁场分布在直角三角形ACD区域内,磁感应强度大小为B,方向垂直于纸面向外,AD边长为2L,θ=30°,质量为m,电荷量为+q的粒子束以不同速度从AD边的中点P垂直AD边沿纸面射入磁场,速率最大的粒子恰好垂直CD边穿出,不考虑粒子的重力,则( )| A. | CD边有粒子射出的区域长一定为$\frac{(3-\sqrt{3})L}{3}$ | |
| B. | 粒子的最大动能为$\frac{{q}^{2}{B}^{2}{L}^{2}}{m}$ | |
| C. | 粒子在磁场中运动的最长时间一定为$\frac{πm}{qB}$ | |
| D. | 粒子在磁场中运动的最短时间为$\frac{πm}{6qB}$ |
7.电子在匀强磁场中的匀速圆周运动,下列说法正确的是( )
| A. | 速率越大,周期越大 | B. | 速率越大,半径越大 | ||
| C. | 速度方向与磁场方向垂直 | D. | 速度方向与洛伦兹力方向平行 |
11.真空中有两个静止的点电荷,它们之间的作用力为F,若它们的带电量都增大为原来的2倍,它们之间的相互作用力变为4F,若只是将距离减少为原来的$\frac{1}{2}$,它们之间的相互作用力变为4F.
12.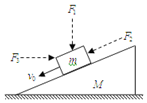 一斜劈静止于粗糙的水平地面上,在其斜面上放一滑块,若给一向下的初速度,则正好保持匀速下滑.如图所示,现在下滑的过程中再加一个作用力,则以下说法正确的是( )
一斜劈静止于粗糙的水平地面上,在其斜面上放一滑块,若给一向下的初速度,则正好保持匀速下滑.如图所示,现在下滑的过程中再加一个作用力,则以下说法正确的是( )
 一斜劈静止于粗糙的水平地面上,在其斜面上放一滑块,若给一向下的初速度,则正好保持匀速下滑.如图所示,现在下滑的过程中再加一个作用力,则以下说法正确的是( )
一斜劈静止于粗糙的水平地面上,在其斜面上放一滑块,若给一向下的初速度,则正好保持匀速下滑.如图所示,现在下滑的过程中再加一个作用力,则以下说法正确的是( )| A. | 加一个竖直向下的力,仍将保持匀速运动,但对地面有摩擦力的作用 | |
| B. | 加一个沿斜面向下的力,则将做加速运动,对地面有水平向左的静摩 擦力的作用 | |
| C. | 加一个水平向右的力,则将做减速运动,在停止前对地有向右的静摩擦力的作用 | |
| D. | 无论在上加什么方向的力,在停止前对地面都无静摩擦力的作用 |
 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造如图所示.设离子源S产生的离子速度很小,可以近似看作为零.产生的离子经过电压为U(未知)的电场加速后,进入一平行板电容器C中,平行板电容器两极间电压为U1,两板间距离为d.板间电场与磁场B1相互垂直,具有某一速度的离子将沿图中虚直线穿过两极板而不发生偏转,而具有其它速度的离子发生偏转而不能射出小孔S1.最后射出小孔S1的离子再进入磁感应强度为B2的匀强磁场,沿着半圆周运动,到达记录它的照相底片上的P点,根据上述材料完成下列问题:
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造如图所示.设离子源S产生的离子速度很小,可以近似看作为零.产生的离子经过电压为U(未知)的电场加速后,进入一平行板电容器C中,平行板电容器两极间电压为U1,两板间距离为d.板间电场与磁场B1相互垂直,具有某一速度的离子将沿图中虚直线穿过两极板而不发生偏转,而具有其它速度的离子发生偏转而不能射出小孔S1.最后射出小孔S1的离子再进入磁感应强度为B2的匀强磁场,沿着半圆周运动,到达记录它的照相底片上的P点,根据上述材料完成下列问题: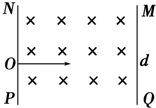 如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长也为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).
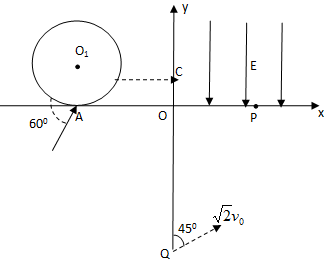
如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长也为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).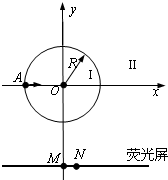 如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x轴正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的N点.求
如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x轴正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的N点.求