如图.正方形容器处在匀强磁场中.一束电子从孔a垂直于磁场沿ab方向射入容器中.其中一部分从c孔射出.一部分从d孔射出.容器处在真空中.下列说法正确的是( )A．从两孔射出的电子速率之比为vc:vd=2:1B．从两孔射出的电子在容器中运动的时间之比tc:td=1:2C．从两孔射出的电子的加速度大小之比ac:ad=$\sqrt{2}$:1D．从两孔射出的电子题目和参考答案——青夏教育精英家教网—

题目内容

5．

如图，正方形容器处在匀强磁场中，一束电子从孔a垂直于磁场沿ab方向射入容器中，其中一部分从c孔射出，一部分从d孔射出，容器处在真空中，下列说法正确的是（　　）

	A．	从两孔射出的电子速率之比为v_c：v_d=2：1
	B．	从两孔射出的电子在容器中运动的时间之比t_c：t_d=1：2
	C．	从两孔射出的电子的加速度大小之比a_c：a_d=$\sqrt{2}$：1
	D．	从两孔射出的电子的加速度大小之比a_c：a_d=2：1

分析由几何关系可知从两孔射出的粒子的运动半径，则由洛仑兹力充当向心力可得出粒子的速度关系；由周期公式及转过的角度可求得时间之比；由向心力公式可求得加速度之比．

解答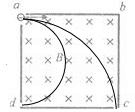解：设磁场边长为a，如图所示，粒子从c点离开，其半径为r_c，粒子从d点离开，其半径为r_d；
A、由Bqv=m$\frac{{v}^{2}}{r}$，得出半径公式r=$\frac{mv}{Bq}$，又由运动轨迹知 r_c=2r_d 则v_c：v_d=2：1，故A正确；
B、由T=$\frac{2πm}{Bq}$，根据圆心角求出运行时间t=$\frac{θ}{2π}$T．运行时间 t_d=$\frac{T}{2}$，t_c=$\frac{T}{4}$．则t_c：t_d=1：2，故B正确．
C、向心加速度：a=$\frac{{v}^{2}}{r}$，则a_c：a_d=2：1，故C错误，D正确；
故选：ABD

点评本题属于带电粒子在磁场中的偏转中典型题目，此类题的关键在于确定圆心及由几何关系求出半径．掌握带电粒子在匀强磁场中做匀速圆周运动的半径公式r=$\frac{mv}{Bq}$，和周期公式T=$\frac{2πm}{Bq}$．

练习册系列答案

（1）该过程中，通过电阻R的电量q；
（2）杆通过OO′时的速度大小；
（3）杆在OO′时，轻绳的拉力大小；
（4）上述过程中，若拉力对杆所做的功为13J，求电阻R上的平均电功率．

16．如图（a）所示，在竖直平面内建立直角坐标系xoy，整个空间内都存在垂直于坐标平面向外的匀强磁场和水平向右的匀强电场，匀强电场的方向与x轴止方向夹角为45⁰．已知带电粒子质量为m、电量为+q，磁感应强度大小为B，电场强度大小E=$\frac{mg}{q}$，重力加速度为g．

（1）若粒子在xoy平面内做匀速直线运动，求粒子的速度v₀；
（2）t=0时刻的电场和磁场方向如图（a）所示，若电场强度和磁感应强度的大小均不变．而方向随时间周期性的改变，如图（b）所示．将该粒子从原点O由静止释放，在0一$\frac{T}{2}$时间内的运动轨迹如图（c）虚线OMN所示，M点为轨迹距y轴的最远点，M距y轴的距离为d．已知在曲线上某一点能找到一个和它内切的半径最大的圆，物体经过此点时，相当于以此圆的半径在做圆周运动，这个圆的半径就定义为曲线上这点的曲率半径．求：
①粒子经过M点时曲率半径ρ
②在图中画出粒子从N点回到O点的轨迹．

13．

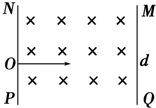如图所示，两个板间存在垂直纸面向里的匀强磁场，一带正电的质子以速度v₀从O点垂直射入．已知两板之间距离为d，板长也为d，O点是NP板的正中点，为使粒子能从两板之间射出，试求磁感应强度B应满足的条件（已知质子带电荷量为q，质量为m）．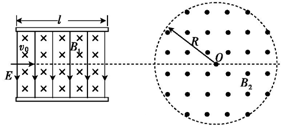

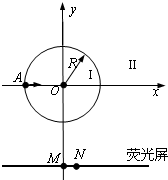20．如图甲所示，在两个水平平行金属极板间存在着竖直向下的匀强电场和垂直于纸面向里的匀强磁场，电场强度和磁感应强度的大小分别为E=2×10⁶ N/C和B₁=0.1T，极板的长度l=$\frac{\sqrt{3}}{3}$m，间距足够大．在板的右侧还存在着另一圆形匀强磁场区域，磁场方向垂直于纸面向外，圆形区域的圆心O位于两平行金属极板的中线上，圆形区域的半径R=$\frac{\sqrt{3}}{3}$m．有一带正电的粒子以某一速度沿极板的中线水平向右飞入极板后恰好做匀速直线运动，然后进入圆形磁场区域，飞出圆形磁场区域后速度方向偏转了60°，不计粒子的重力，粒子的比荷$\frac{q}{m}$=2×10⁸ C/kg．

（1）求粒子沿极板的中线飞入的初速度v₀．
（2）求圆形区域磁场的磁感应强度B₂的大小．
（3）在其他条件都不变的情况下，将极板间的磁场B₁撤去，为使粒子飞出极板后不能进入圆形磁场区域，求圆形区域的圆心O离极板右边缘的水平距离d应满足的条件．

10．

如图所示，圆心为原点、半径为R的圆将xOy平面分为两个区域，即圆内区域Ⅰ和圆外区域Ⅱ．区域Ⅰ内有方向垂直于xOy平面的匀强磁场B₁．平行于x轴的荧光屏垂直于xOy平面，放置在坐标y=-2.2R的位置．一束质量为m、电荷量为q、动能为E₀的带正电粒子从坐标为（-R，0）的A点沿x轴正方向射入区域Ⅰ，当区域Ⅱ内无磁场时，粒子全部打在荧光屏上坐标为（0，-2.2R）的M点，且此时，若将荧光屏沿y轴负方向平移，粒子打在荧光屏上的位置不变．若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B₂，上述粒子仍从A点沿x轴正方向射入区域Ⅰ，则粒子全部打在荧光屏上坐标为（0.4R，-2.2R）的N点．求
（1）打在M点和N点的粒子运动速度v₁、v₂的大小．
（2）在区域Ⅰ和Ⅱ中磁感应强度B₁、B₂的大小和方向．
（3）若将区域Ⅱ中的磁场撤去，换成平行于x轴的匀强电场，仍从A点沿x轴正方向射入区域Ⅰ的粒子恰好也打在荧光屏上的N点，则电场的场强为多大？

17．

匀强磁场分布在直角三角形ACD区域内，磁感应强度大小为B，方向垂直于纸面向外，AD边长为2L，θ=30°，质量为m，电荷量为+q的粒子束以不同速度从AD边的中点P垂直AD边沿纸面射入磁场，速率最大的粒子恰好垂直CD边穿出，不考虑粒子的重力，则（　　）

	A．	CD边有粒子射出的区域长一定为$\frac{（3-\sqrt{3}）L}{3}$
	B．	粒子的最大动能为$\frac{{q}^{2}{B}^{2}{L}^{2}}{m}$
	C．	粒子在磁场中运动的最长时间一定为$\frac{πm}{qB}$
	D．	粒子在磁场中运动的最短时间为$\frac{πm}{6qB}$

14．如图所示平面直角坐标系xoy，P点在x轴上，OP距离为L，Q点在y轴负方向上某处；在第一象限有平行y轴的匀强电场，第二象限内有一圆形区域与x轴相切于A点，圆形区域的半径为L，在第四象限未知的矩形区域（图中未画出），圆形区域和矩形区域有相同的匀强磁场，磁场垂直于xoy平面（图中未画出），电荷量为+q，质量为m、速度大小v₀的粒子a从A点与x轴成60⁰角进入圆形磁场，出磁场后垂直y轴经C点进入电场，再从P点出射；质量为m、电荷量为-q、速率为$\sqrt{2}$v₀的粒子b，从Q点向与y轴成45^°角方向发射，经过并离开矩形磁场区域后与P点出射的粒子a相碰，相碰时粒子速度方向相反，不计粒子重力和粒子间相互作用力，求：

（1）圆形区域内的磁感应强度大小和方向；
（2）第一象限的电场强度大小；
（3）矩形区域的最小面积．

15．下列说法正确的是（　　）

	A．	研究跳水运动员转体动作时，运动员不可视为质点
	B．	位移和路程都是矢量
	C．	质点通过一段路程，位移不可能是零
	D．	速度减小时，加速度也一定减小

试题分类