题目内容
1.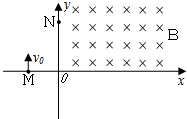 如图,在xoy平面内,第一象限内存在着方向垂直于xoy平面向里的匀强磁场,第二象限内存在着平行于x轴的匀强电场(图中未画出),一质量为m,电荷量为-q的粒子(不计重力),从直角坐标系x轴上的M点以v0的速度平行于y轴正方向射出,M点距坐标原点的距离为d,带电粒子经电场偏转后从y轴上N点进入第一象限,N点距坐标原点的距离为2d,带电粒子通过第一象限的磁场后,垂直于x轴进入第四象限.求:
如图,在xoy平面内,第一象限内存在着方向垂直于xoy平面向里的匀强磁场,第二象限内存在着平行于x轴的匀强电场(图中未画出),一质量为m,电荷量为-q的粒子(不计重力),从直角坐标系x轴上的M点以v0的速度平行于y轴正方向射出,M点距坐标原点的距离为d,带电粒子经电场偏转后从y轴上N点进入第一象限,N点距坐标原点的距离为2d,带电粒子通过第一象限的磁场后,垂直于x轴进入第四象限.求:(1)电场强度E的大小和方向;
(2)磁感应强度为B的大小和粒子在第一象限运动的时间;
(3)若要使带电粒子从第四象限垂直于y轴进入第三象限,在第四象限内加有一圆形区域的匀强磁场,磁场方向垂直于xoy平面向里,所加磁场的磁感应强度是第一象限磁感应强度的两倍,求此圆形区域的最小面积.
分析 (1)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出电场强度.
(2)求出粒子在磁场中转过的圆心角,然后根据粒子做圆周运动的周期求出粒子的运动时间.
(3)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律与几何知识求出磁场的最小半径,然后求出最小面积.
解答 解:(1)带电粒子在电场中做类平抛运动,设其运动的时间为t
则有:2d=v0t,d=$\frac{1}{2}$at2=$\frac{1}{2}$$\frac{qE}{m}$t2,解得:E=$\frac{m{v}_{0}^{2}}{2qd}$;
带电粒子受力方向向右,粒子带负电,因此电场方向应为x负方向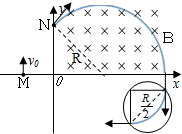 ;
;
(2)带电粒子运动至N点时,其竖直速度:vy=v0,水平速度:vx=at=v0,
故带电粒子运动至N点时的速度:v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{2}$v0,方向:与y轴成450夹角;
又带电粒子垂直于x轴进入第四象限,由几何知识可知(如图所示),
带电粒子在第一象限做圆周运动的圆心在x轴上,其运动半径:R=2$\sqrt{2}$d,
带电粒子在第一象限转过的圆心角为135°;
因此,带电粒子在第一象限的运动时间为:t′=$\frac{θ}{360°}$T=$\frac{135°}{360°}$×$\frac{2πR}{v}$=$\frac{3πd}{2{v}_{0}}$;
(3)要使带电粒子从第四象限垂直于y轴进入第三象限,则带电粒子在磁场中必定转过90°,如图所示,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{R}$,解得:R=$\frac{mv}{qB}$,第四象限内磁感应强度是第一象限磁感应强度的两倍,
因此带电粒子在第四象限中运动的半径为$\frac{R}{2}$,所以所加圆形磁场的最小半径为:r=$\frac{\sqrt{2}}{2}$×$\frac{R}{2}$=d,
因此此圆形区域的最小面积为:Smin=πr2=πd2.
答:(1)电场强度E的大小为$\frac{m{v}_{0}^{2}}{2qd}$,方向:沿x轴负方向;
(2)磁感应强度为B的大小和粒子在第一象限运动的时间为$\frac{3πd}{2{v}_{0}}$;
(3)此圆形区域的最小面积为πd2.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程是解题的前提与关键,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题;解题时注意几何知识的应用;处理带电粒子在磁场中运动的基本思路是:作出运动轨迹,确定圆心,求半径、求圆心角,然后应用牛顿第二定律求解.

 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造如图所示.设离子源S产生的离子速度很小,可以近似看作为零.产生的离子经过电压为U(未知)的电场加速后,进入一平行板电容器C中,平行板电容器两极间电压为U1,两板间距离为d.板间电场与磁场B1相互垂直,具有某一速度的离子将沿图中虚直线穿过两极板而不发生偏转,而具有其它速度的离子发生偏转而不能射出小孔S1.最后射出小孔S1的离子再进入磁感应强度为B2的匀强磁场,沿着半圆周运动,到达记录它的照相底片上的P点,根据上述材料完成下列问题:
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造如图所示.设离子源S产生的离子速度很小,可以近似看作为零.产生的离子经过电压为U(未知)的电场加速后,进入一平行板电容器C中,平行板电容器两极间电压为U1,两板间距离为d.板间电场与磁场B1相互垂直,具有某一速度的离子将沿图中虚直线穿过两极板而不发生偏转,而具有其它速度的离子发生偏转而不能射出小孔S1.最后射出小孔S1的离子再进入磁感应强度为B2的匀强磁场,沿着半圆周运动,到达记录它的照相底片上的P点,根据上述材料完成下列问题: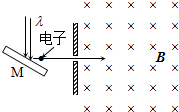 波长为λ的单色光照射某金属M表面产生光电效应,发射的光电子(电量绝对值为e,质量为m)经狭缝s后垂直进入磁感应强度为B的均匀磁场,如图所示.今已测出电子在该磁场中作圆运动的最大半径为R,求:
波长为λ的单色光照射某金属M表面产生光电效应,发射的光电子(电量绝对值为e,质量为m)经狭缝s后垂直进入磁感应强度为B的均匀磁场,如图所示.今已测出电子在该磁场中作圆运动的最大半径为R,求:
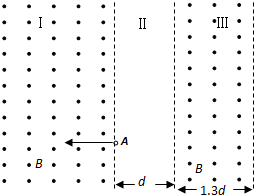 如图所示,一个带正电的粒子沿磁场边界从A点射入左侧磁场,粒子质量为m,电荷量为q,其中区域Ⅰ、Ⅲ内是垂直纸面向外的匀强磁场,左边区域足够大,右边区域宽度为1.3d,磁感应强度大小均为B,区域Ⅱ是两磁场间的无场区,两条竖直虚线是其边界线,宽度为d;粒子从左边界线A点射入磁场后,经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点,若粒子在左侧磁场中的半径为d,整个装置在真空中,不计粒子的重力.
如图所示,一个带正电的粒子沿磁场边界从A点射入左侧磁场,粒子质量为m,电荷量为q,其中区域Ⅰ、Ⅲ内是垂直纸面向外的匀强磁场,左边区域足够大,右边区域宽度为1.3d,磁感应强度大小均为B,区域Ⅱ是两磁场间的无场区,两条竖直虚线是其边界线,宽度为d;粒子从左边界线A点射入磁场后,经过Ⅰ、Ⅱ、Ⅲ区域后能回到A点,若粒子在左侧磁场中的半径为d,整个装置在真空中,不计粒子的重力.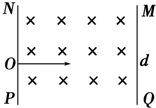 如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长也为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).
如图所示,两个板间存在垂直纸面向里的匀强磁场,一带正电的质子以速度v0从O点垂直射入.已知两板之间距离为d,板长也为d,O点是NP板的正中点,为使粒子能从两板之间射出,试求磁感应强度B应满足的条件(已知质子带电荷量为q,质量为m).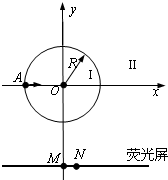 如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x轴正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的N点.求
如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ.区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1.平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x轴正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变.若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的N点.求