题目内容
18. 如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )| A. | m$\sqrt{{g^2}-{{(\frac{F}{M+m})}^2}}$ | B. | m$\sqrt{{g^2}+{{(\frac{F}{M+m})}^2}}$ | C. | m$\sqrt{{g^2}+{{(\frac{F}{m})}^2}}$ | D. | $\sqrt{{{(mg)}^2}+{F^2}}$ |
分析 先以整体为研究对象,根据牛顿第二定律求出加速度,再对小球研究,求出椭圆面对小球的支持力大小,由牛顿第三定律得到小球对椭圆面的压力大小.
解答 解: 先以整体为研究对象,根据牛顿第二定律得:加速度为a=$\frac{F}{M+m}$
先以整体为研究对象,根据牛顿第二定律得:加速度为a=$\frac{F}{M+m}$
再对小球研究,分析受力情况,如图,由牛顿第二定律得到:
N=$\sqrt{(mg)^{2}+(ma)^{2}}$=m$\sqrt{{g}^{2}+(\frac{F}{M+m})^{2}}$
故选:B
点评 本题是连接体问题,两个物体的加速度相同,采用整体法和隔离法相结合进行研究.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图所示,有一圆形匀强磁场区域,O为圆的圆心,磁场方向垂直纸面向里.两个正、负电子a、b,以不同的速率沿着PO方向进入磁场,运动轨迹如图所示.不计电子之间的相互作用及重力.a与b比较,下列判断正确的是( )
如图所示,有一圆形匀强磁场区域,O为圆的圆心,磁场方向垂直纸面向里.两个正、负电子a、b,以不同的速率沿着PO方向进入磁场,运动轨迹如图所示.不计电子之间的相互作用及重力.a与b比较,下列判断正确的是( )
 如图所示,有一圆形匀强磁场区域,O为圆的圆心,磁场方向垂直纸面向里.两个正、负电子a、b,以不同的速率沿着PO方向进入磁场,运动轨迹如图所示.不计电子之间的相互作用及重力.a与b比较,下列判断正确的是( )
如图所示,有一圆形匀强磁场区域,O为圆的圆心,磁场方向垂直纸面向里.两个正、负电子a、b,以不同的速率沿着PO方向进入磁场,运动轨迹如图所示.不计电子之间的相互作用及重力.a与b比较,下列判断正确的是( )| A. | a为正电子,b为负电子 | B. | b的速率较大 | ||
| C. | a在磁场中所受洛伦兹力较大 | D. | b在磁场中运动的时间较长 |
9. AB是固定在空中的光滑水平横杆,一质量为M的物块穿在杆AB上,物块通过细线悬吊着一质量为m的小球.现用沿杆的恒力F拉物块使物块、小球一起(保持相对静止)向右运动,细线与竖直方向夹角为θ,则以下说法正确的是( )
AB是固定在空中的光滑水平横杆,一质量为M的物块穿在杆AB上,物块通过细线悬吊着一质量为m的小球.现用沿杆的恒力F拉物块使物块、小球一起(保持相对静止)向右运动,细线与竖直方向夹角为θ,则以下说法正确的是( )
 AB是固定在空中的光滑水平横杆,一质量为M的物块穿在杆AB上,物块通过细线悬吊着一质量为m的小球.现用沿杆的恒力F拉物块使物块、小球一起(保持相对静止)向右运动,细线与竖直方向夹角为θ,则以下说法正确的是( )
AB是固定在空中的光滑水平横杆,一质量为M的物块穿在杆AB上,物块通过细线悬吊着一质量为m的小球.现用沿杆的恒力F拉物块使物块、小球一起(保持相对静止)向右运动,细线与竖直方向夹角为θ,则以下说法正确的是( )| A. | 杆对物块的支持力为Mg | B. | 细线上的拉力为$\frac{mg}{sinθ}$ | ||
| C. | F=(M+m)gtanθ | D. | 物块和小球的加速度为gsinθ |
10. 质量为M的三角形物块放置在粗糙水平地面上,开始质量为m的物体以速度v0沿三角形物块的粗糙斜面匀速下滑,某时刻给物体施加一沿斜面向下的推力F,使物体沿斜面向下做加速运动,如图所示.整个过程中,三角形物块始终静止在地面上,设物体向下加速运动时,地面对三角形物块的支持力大小为N,地面对三角形物块的摩擦力的大小为,重力加速度为g,则( )
质量为M的三角形物块放置在粗糙水平地面上,开始质量为m的物体以速度v0沿三角形物块的粗糙斜面匀速下滑,某时刻给物体施加一沿斜面向下的推力F,使物体沿斜面向下做加速运动,如图所示.整个过程中,三角形物块始终静止在地面上,设物体向下加速运动时,地面对三角形物块的支持力大小为N,地面对三角形物块的摩擦力的大小为,重力加速度为g,则( )
 质量为M的三角形物块放置在粗糙水平地面上,开始质量为m的物体以速度v0沿三角形物块的粗糙斜面匀速下滑,某时刻给物体施加一沿斜面向下的推力F,使物体沿斜面向下做加速运动,如图所示.整个过程中,三角形物块始终静止在地面上,设物体向下加速运动时,地面对三角形物块的支持力大小为N,地面对三角形物块的摩擦力的大小为,重力加速度为g,则( )
质量为M的三角形物块放置在粗糙水平地面上,开始质量为m的物体以速度v0沿三角形物块的粗糙斜面匀速下滑,某时刻给物体施加一沿斜面向下的推力F,使物体沿斜面向下做加速运动,如图所示.整个过程中,三角形物块始终静止在地面上,设物体向下加速运动时,地面对三角形物块的支持力大小为N,地面对三角形物块的摩擦力的大小为,重力加速度为g,则( )| A. | f≠0,N>(m+M)g | B. | f=0,N=(m+M)g | C. | f≠0,N<(m+M)g | D. | f=0,N>(m+M)g |
7. 如图所示,表面光滑的T型支架可绕O点无摩擦自由转动,B端搁在水平地面上,将一小物体放在支架上让其从A端自由下滑,当小物体经过C点时,B端受到的弹力为N1;若将该小物体放在支架上,从B端给小物体一定的初速度让其上滑,当小物体经过C点时,B端受到的弹力为N2,前后两次过程T型支架均不翻转,则( )
如图所示,表面光滑的T型支架可绕O点无摩擦自由转动,B端搁在水平地面上,将一小物体放在支架上让其从A端自由下滑,当小物体经过C点时,B端受到的弹力为N1;若将该小物体放在支架上,从B端给小物体一定的初速度让其上滑,当小物体经过C点时,B端受到的弹力为N2,前后两次过程T型支架均不翻转,则( )
 如图所示,表面光滑的T型支架可绕O点无摩擦自由转动,B端搁在水平地面上,将一小物体放在支架上让其从A端自由下滑,当小物体经过C点时,B端受到的弹力为N1;若将该小物体放在支架上,从B端给小物体一定的初速度让其上滑,当小物体经过C点时,B端受到的弹力为N2,前后两次过程T型支架均不翻转,则( )
如图所示,表面光滑的T型支架可绕O点无摩擦自由转动,B端搁在水平地面上,将一小物体放在支架上让其从A端自由下滑,当小物体经过C点时,B端受到的弹力为N1;若将该小物体放在支架上,从B端给小物体一定的初速度让其上滑,当小物体经过C点时,B端受到的弹力为N2,前后两次过程T型支架均不翻转,则( )| A. | N1=N2 | B. | N1<N2 | C. | N1>N2 | D. | N1=0 |
8. 一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )
一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )
 一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )
一小滑块(可看成质点)在水平拉力F作用下,沿粗糙水平面上做直线运动,其速度v随时间t变化的图象如图所示.在0.5s、1.5s、2.5s、3.5s时刻拉力F的大小分别为F1、F2、F3、F4,则下列判断一定正确的是( )| A. | F1<F2 | B. | F2=F3 | C. | F1>F4 | D. | F3>F4 |
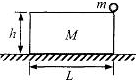 如图所示,一上表面光滑的矩形滑块置于水平地面上,其质量M=2kg,长L=2m,高h=0.8m,滑块与地面间动摩擦因数μ=0.2,在滑块的右端放置一质量m=1kg的小球.现用外力击打滑块左端,使其在极短时间内获得v0=4m/s的水平向右速度,经过一段时间后小球落地.(g取10m/s2)试求:
如图所示,一上表面光滑的矩形滑块置于水平地面上,其质量M=2kg,长L=2m,高h=0.8m,滑块与地面间动摩擦因数μ=0.2,在滑块的右端放置一质量m=1kg的小球.现用外力击打滑块左端,使其在极短时间内获得v0=4m/s的水平向右速度,经过一段时间后小球落地.(g取10m/s2)试求:
