题目内容
3.如图甲所示,一质量m=2kg的物块静止于水平面上,t=0时刻物块开始受到水平方向作用力,力的大小随时间变化的关系如图乙所示,物块与水平面的动摩擦因数为μ=0.1,g取10m/s2.求:(1)前4s内物块的位移s1;
(2)6s后物块还能继续运动的时间t3;
(3)在图丙中画出物块整个运动过程的v-t图象.

分析 (1)以物体为研究对象进行受力分析,根据牛顿第二定律求解加速度,再根据位移时间关系求解位移;
(2)求出4s~6s的加速度和6s末的速度,再求出6s以后的加速度,根据速度时间关系求解静止时间;
(3)根据运动情况画出速度图象.
解答 解:(1)前4秒内物体的受力情况如图所示: 根据牛顿第二定律可得:F1-μmg=ma1,
根据牛顿第二定律可得:F1-μmg=ma1,
解得:a1=$\frac{{F}_{1}}{m}-μg=(\frac{8}{2}-1)m/{s}^{2}=3m/{s}^{2}$,
根据运动学计算公式可得:s1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$=$\frac{1}{2}×3×16m=24m$;
(2)4s~6s内物体的受力情况如图所示, 根据牛顿第二定律可得:F2+μmg=ma2,
根据牛顿第二定律可得:F2+μmg=ma2,
解得:a2=$\frac{{F}_{2}}{m}+μg=(\frac{8}{2}+1)m/{s}^{2}=5m/{s}^{2}$,
4s时的速度为v1=a1t1=3×4m/s=12m/s,
6s时的速度为:v2=v1-a2t2=12-5×2=2m/s;
以后物体运动的加速度a3=μg=1m/s2,
所以减速到零还要经过t3=$\frac{{v}_{2}}{{a}_{3}}=\frac{2}{1}s=2s$,
所以6s后物块还能继续运动的时间为2s;
(3)根据运动情况可得其速度图象如图所示.
答:(1)前4s内物块的位移为24m;
(2)6s后物块还能继续运动的时间为2s;
(3)图象见解析.
点评 对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.

练习册系列答案
相关题目
6. 如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
 如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住.现用一个恒力F拉斜面,使斜面在水平面上向右做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )| A. | 若加速度足够小,竖直挡板对球的弹力可能为零 | |
| B. | 若加速度足够大,斜面对球的弹力可能为零 | |
| C. | 斜面对球的弹力大小与加速度大小无关 | |
| D. | 挡板对球的弹力大小与加速度大小无关 |
14. 在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )
在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )
 在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )
在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )| A. | M的带电量比N的大 | B. | M带正电荷、N带负电荷 | ||
| C. | 移动过程中匀强电场对M做负功 | D. | 移动过程中匀强电场对N做正功 |
11. 如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )
如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )
 如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )
如图所示,水平地面上固定一足够长的光滑斜面(空气阻力不计),质量为m的小球以初速度v0从斜面底端冲上斜面,在小球沿斜面向上运动的过程中( )| A. | 小球以速度v0沿斜面做匀速直线运动 | |
| B. | 小球受到重力、斜面的支持力、沿斜面向上的冲力 | |
| C. | 小球受到的支持力大小为mgsinθ | |
| D. | 小球受到的支持力大小为mgcosθ |
18. 如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
 如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )| A. | m$\sqrt{{g^2}-{{(\frac{F}{M+m})}^2}}$ | B. | m$\sqrt{{g^2}+{{(\frac{F}{M+m})}^2}}$ | C. | m$\sqrt{{g^2}+{{(\frac{F}{m})}^2}}$ | D. | $\sqrt{{{(mg)}^2}+{F^2}}$ |
 如图,在宽为l,足够长的水平虚线内有垂直纸面向里的匀强磁场,其上方距上边界h处有一导线框(各边长如图中标注),现将导线框由静止释放,从线框下边进入磁场开始计时至线框完全离开磁场(整个过程线框保持竖直且不翻转).该过程中v-t图线可能正确的是( )
如图,在宽为l,足够长的水平虚线内有垂直纸面向里的匀强磁场,其上方距上边界h处有一导线框(各边长如图中标注),现将导线框由静止释放,从线框下边进入磁场开始计时至线框完全离开磁场(整个过程线框保持竖直且不翻转).该过程中v-t图线可能正确的是( )



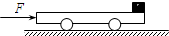 光滑的水平面上静置一足够长、质量M=8kg的小车,如图所示.现在小车的左端施加一大小F=8N的水平推力,当小车向右运动的速度达到v0=1.5m/s时,在小车右端轻轻地放上一质量m=2kg的小物块(可视为质点).已知小物块与小车间的动摩擦因数μ=0.2,取g=10m/s2.求:
光滑的水平面上静置一足够长、质量M=8kg的小车,如图所示.现在小车的左端施加一大小F=8N的水平推力,当小车向右运动的速度达到v0=1.5m/s时,在小车右端轻轻地放上一质量m=2kg的小物块(可视为质点).已知小物块与小车间的动摩擦因数μ=0.2,取g=10m/s2.求: 如图,一质量m=1kg的橡胶块,在与斜面成α=37°角的F=5N的拉力作用下,以v0=12m/s的初速度从A点开始沿斜面向上做匀变速运动,经t=2s的时间运动了L=12m的距离到达B点.斜面倾角θ=30°,重力加速度g取10m/s2.(已知sin37°=0.6,cos37°=0.8).求:
如图,一质量m=1kg的橡胶块,在与斜面成α=37°角的F=5N的拉力作用下,以v0=12m/s的初速度从A点开始沿斜面向上做匀变速运动,经t=2s的时间运动了L=12m的距离到达B点.斜面倾角θ=30°,重力加速度g取10m/s2.(已知sin37°=0.6,cos37°=0.8).求: 某快递公司分拣邮件的水平传输装置示意如图,皮带在电动机的带动下保持v=1m/s的恒定速度向右运动,现将一质量为m=2kg的邮件轻放在皮带上,邮件和皮带间的动摩擦因数μ=0.5.设皮带足够长,取g=10m/s2,在邮件与皮带发生相对滑动过程中,求:
某快递公司分拣邮件的水平传输装置示意如图,皮带在电动机的带动下保持v=1m/s的恒定速度向右运动,现将一质量为m=2kg的邮件轻放在皮带上,邮件和皮带间的动摩擦因数μ=0.5.设皮带足够长,取g=10m/s2,在邮件与皮带发生相对滑动过程中,求: