题目内容
9. AB是固定在空中的光滑水平横杆,一质量为M的物块穿在杆AB上,物块通过细线悬吊着一质量为m的小球.现用沿杆的恒力F拉物块使物块、小球一起(保持相对静止)向右运动,细线与竖直方向夹角为θ,则以下说法正确的是( )
AB是固定在空中的光滑水平横杆,一质量为M的物块穿在杆AB上,物块通过细线悬吊着一质量为m的小球.现用沿杆的恒力F拉物块使物块、小球一起(保持相对静止)向右运动,细线与竖直方向夹角为θ,则以下说法正确的是( )| A. | 杆对物块的支持力为Mg | B. | 细线上的拉力为$\frac{mg}{sinθ}$ | ||
| C. | F=(M+m)gtanθ | D. | 物块和小球的加速度为gsinθ |
分析 以整体为研究对象竖直方向根据共点力的平衡条件计算支持力大小;以小球为研究对象,根据牛顿第二定律求解加速度,水平方向以整体为研究对象根据牛顿第二定律求解拉力大小.
解答 解:A、以整体为研究对象,竖直方向受力平衡,则可知杆对物块的支持力为(M+m)g,A错误;
B、以m为研究对象进行受力分析如图所示,
由此可得细线的拉力T=$\frac{mg}{cosθ}$,B错误;
CD、小球运动的加速度为:a=gtanθ,以整体为研究对象,整体的加速度为gtanθ,水平方向根据牛顿第二定律可得:F=(M+m)a=(M+m)gtanθ,C正确、D错误;
故选:C.
点评 本题主要是考查了牛顿第二定律的知识;利用牛顿第二定律答题时的一般步骤是:确定研究对象、进行受力分析、进行正交分解、在坐标轴上利用牛顿第二定律建立方程进行解答;注意整体法和隔离法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图所示,一理想变压器的原副线圈匝数比为n1:n2=10:1,一阻值为10Ω的电阻R连接在变压器的副线圈上.若加在原线圈上的电压瞬时值随时间变化规律为u=100$\sqrt{2}$cosl00πt(V),下列说法中正确的是( )
如图所示,一理想变压器的原副线圈匝数比为n1:n2=10:1,一阻值为10Ω的电阻R连接在变压器的副线圈上.若加在原线圈上的电压瞬时值随时间变化规律为u=100$\sqrt{2}$cosl00πt(V),下列说法中正确的是( )
 如图所示,一理想变压器的原副线圈匝数比为n1:n2=10:1,一阻值为10Ω的电阻R连接在变压器的副线圈上.若加在原线圈上的电压瞬时值随时间变化规律为u=100$\sqrt{2}$cosl00πt(V),下列说法中正确的是( )
如图所示,一理想变压器的原副线圈匝数比为n1:n2=10:1,一阻值为10Ω的电阻R连接在变压器的副线圈上.若加在原线圈上的电压瞬时值随时间变化规律为u=100$\sqrt{2}$cosl00πt(V),下列说法中正确的是( )| A. | 电压表的示数为10$\sqrt{2}$V | B. | 变压器的输入功率为10W | ||
| C. | 电流表的示数为0.1 A | D. | 交变电流的频率为100 Hz |
13.一足够长水平浅色传送带以v0=4m/s匀速运动,现将一可视为质点的小煤块轻放在其上方,已知煤块与传送带间的动摩擦因数为μ=0.2.经过一定时间后达到共同速度.令传送带突然停下,以后不再运动,到最后煤块也停下.已知重力加速度为g=10m/s2.则( )
| A. | 煤块经过时间t=4s与皮带第一次共速 | |
| B. | 煤块在传送带上划出的轨迹长度为8米 | |
| C. | 煤块在传送带上划出的轨迹长度为4米 | |
| D. | 煤块经过时间t=2s距离出发点最远 |
10.A、B、C为三个相同的金属小球,A、B带等量的同种电荷,作用力为F,C不带电,让C先与A接触后再与B接触,然后移开,则A、B间的作用力是( )
| A. | 斥力,$\frac{3F}{8}$ | B. | 斥力,$\frac{F}{8}$ | C. | 0 | D. | 引力,$\frac{F}{4}$ |
4. 如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )
如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )
 如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )
如图,质量m=10kg的物块甲与质量为M=4kg长木板(足够长)乙一起在外力F的作用下向右做匀速运动,已知甲、乙之间动摩擦因数μ1=0.1,地面和长木板之间动摩擦因数μ2=0.2,则撤掉力F后(由于木板足够长,甲不会脱离木板),则下列说法错误的是( )| A. | 甲乙仍然相对静止,一起匀减速运动直至停止 | |
| B. | 在甲停止运动前,地面对乙的摩擦力大小始终不变 | |
| C. | 在甲停止运动前,乙的加速大小都是4.5m/s2 | |
| D. | 在乙停止运动前,甲的加速度大小始终为1m/s2 |
14. 在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )
在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )
 在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )
在水平匀强电场中,将两个不计重力的带电小球M和N分别沿图示路径移动到同一水平线上的不同位置,释放后,M、N保持静止,则( )| A. | M的带电量比N的大 | B. | M带正电荷、N带负电荷 | ||
| C. | 移动过程中匀强电场对M做负功 | D. | 移动过程中匀强电场对N做正功 |
1.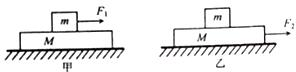 质量均为M的两木板放在光滑水平面上,两木板的中点各放置完全相同、质量均为m的物块,已知M>m.现从静止开始分别在物块和木板上各作用水平恒力F1、F2,如图甲、乙所示.已知物块和木板之间的动摩擦因数相同,两木板长度也相同.下列说法正确的是( )
质量均为M的两木板放在光滑水平面上,两木板的中点各放置完全相同、质量均为m的物块,已知M>m.现从静止开始分别在物块和木板上各作用水平恒力F1、F2,如图甲、乙所示.已知物块和木板之间的动摩擦因数相同,两木板长度也相同.下列说法正确的是( )
 质量均为M的两木板放在光滑水平面上,两木板的中点各放置完全相同、质量均为m的物块,已知M>m.现从静止开始分别在物块和木板上各作用水平恒力F1、F2,如图甲、乙所示.已知物块和木板之间的动摩擦因数相同,两木板长度也相同.下列说法正确的是( )
质量均为M的两木板放在光滑水平面上,两木板的中点各放置完全相同、质量均为m的物块,已知M>m.现从静止开始分别在物块和木板上各作用水平恒力F1、F2,如图甲、乙所示.已知物块和木板之间的动摩擦因数相同,两木板长度也相同.下列说法正确的是( )| A. | 甲图中,无沦F1的大小如何,只要F1作用时间足够长,则物块和木板就可分离 | |
| B. | 乙图中,只有F2的大小大于某一值时,才可能使物块和木板分离 | |
| C. | 使物块和木板分离的最小作用力F1>F2 | |
| D. | 使物块和木板分离的最小作用力F1<F2 |
18. 如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
 如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )
如图,一截面为椭圆形的容器内壁光滑其质量为M,置于光滑水平面上,内有一质量为m的小球,当容器受到一个水平向右的力F作用向右匀加速运动时,小球处于图示位置,此时小球对椭圆面的压力大小为( )| A. | m$\sqrt{{g^2}-{{(\frac{F}{M+m})}^2}}$ | B. | m$\sqrt{{g^2}+{{(\frac{F}{M+m})}^2}}$ | C. | m$\sqrt{{g^2}+{{(\frac{F}{m})}^2}}$ | D. | $\sqrt{{{(mg)}^2}+{F^2}}$ |
19. 如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
 如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )
如图所示,三角体由两种材料拼接而成,BC界面平行底面DE,两侧面与水平面夹角分别为30°和60°.已知物块从A静止下滑,加速至B匀速至D;若该物块静止从A沿另一侧面下滑,则有( )| A. | 通过C点的速率可能等于通过B点的速率 | |
| B. | AB段的运动时间大于AC段的运动时间 | |
| C. | 物块将加速至C匀速至E | |
| D. | 一直加速运动到E,但AC段的加速度比CE段小 |