题目内容
14. 两条足够长的光滑金属导轨间距为L=0.5m,与水平面夹角为θ=37°,空间存在垂直于导轨平面向下的匀强磁场,磁感应强度B=2T,导体棒ab与导轨接触良好,质量为m=0.1kg,电阻R=4Ω,回路中其他部分电阻不计,现开关S断开,由静止释放导体棒后闭合S,已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
两条足够长的光滑金属导轨间距为L=0.5m,与水平面夹角为θ=37°,空间存在垂直于导轨平面向下的匀强磁场,磁感应强度B=2T,导体棒ab与导轨接触良好,质量为m=0.1kg,电阻R=4Ω,回路中其他部分电阻不计,现开关S断开,由静止释放导体棒后闭合S,已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)稳定后导体棒的速度;
(2)回路中最大热功率.
分析 (1)当导体棒加速度为零时,导体棒达到稳定,做匀速直线运动,根据平衡,结合安培力的表达式求出导体棒的速度.
(2)当导体棒速度最大时,即稳定时,回路中产生的功率最大,根据能量守恒求出回路中最大热功率.
解答 解:(1)当导体棒加速度为零时,速度最大,达到稳定,有:
mgsinθ=BIL=$\frac{{B}^{2}{L}^{2}v}{R}$,
解得:v=$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$.
(2)当导体棒匀速运动时,回路中的功率最大,根据能量守恒知,重力的功率等于回路中的热功率,为:
P=P热=mgvsinθ=$\frac{{m}^{2}{g}^{2}Rsi{n}^{2}θ}{{B}^{2}{L}^{2}}$.
答:(1)稳定后导体棒的速度为$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$;
(2)回路中最大热功率为$\frac{{m}^{2}{g}^{2}Rsi{n}^{2}θ}{{B}^{2}{L}^{2}}$..
点评 本题考查了电磁感应与力学和能量的综合运用,知道导体棒加速度为零时,速度最大,对于第二问,也可以结合热功率公式,运用欧姆定律进行求解.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
20.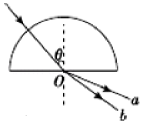 如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
 如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )
如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后出a、b两束光线.则( )| A. | 在玻璃中,a光的传播速度小于b光的传播速度 | |
| B. | 在真空中,a光的波长小于b光的波长 | |
| C. | 玻璃砖对a光的折射率小于b光的折射率 | |
| D. | 若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失 | |
| E. | 分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距 |
1. 如图所示,光滑水平面上并排放两个完全相同的可以视为质点的物体A和B,其中物块A被一条弹性绳(遵守胡克定律)连接,绳的另一端固定在高处O点,物体A在O点正下方时,弹性绳处于原长.已知弹性绳原长为l,劲度系数为k.现使A、B一起从绳和竖直方向夹角为θ=60°开始由静止释放,下列说法正确的是( )
如图所示,光滑水平面上并排放两个完全相同的可以视为质点的物体A和B,其中物块A被一条弹性绳(遵守胡克定律)连接,绳的另一端固定在高处O点,物体A在O点正下方时,弹性绳处于原长.已知弹性绳原长为l,劲度系数为k.现使A、B一起从绳和竖直方向夹角为θ=60°开始由静止释放,下列说法正确的是( )
 如图所示,光滑水平面上并排放两个完全相同的可以视为质点的物体A和B,其中物块A被一条弹性绳(遵守胡克定律)连接,绳的另一端固定在高处O点,物体A在O点正下方时,弹性绳处于原长.已知弹性绳原长为l,劲度系数为k.现使A、B一起从绳和竖直方向夹角为θ=60°开始由静止释放,下列说法正确的是( )
如图所示,光滑水平面上并排放两个完全相同的可以视为质点的物体A和B,其中物块A被一条弹性绳(遵守胡克定律)连接,绳的另一端固定在高处O点,物体A在O点正下方时,弹性绳处于原长.已知弹性绳原长为l,劲度系数为k.现使A、B一起从绳和竖直方向夹角为θ=60°开始由静止释放,下列说法正确的是( )| A. | 刚释放时物块A对B的推力为$\frac{\sqrt{3}}{4}$kl | |
| B. | 物块A向右运动的最大距离为2$\sqrt{3}$l | |
| C. | 从静止开始到A、B分离时,绳子对A做功大于A对B做的功 | |
| D. | 从静止开始到A、B分离时,绳子对A的冲量等于A对B的冲量 |
3. 在如图所示的电路中,调节滑动变阻器的阻值,电源路端电压U随滑动变阻器阻值R的变化关系图象如图乙所示,下列说法正确的是( )
在如图所示的电路中,调节滑动变阻器的阻值,电源路端电压U随滑动变阻器阻值R的变化关系图象如图乙所示,下列说法正确的是( )
 在如图所示的电路中,调节滑动变阻器的阻值,电源路端电压U随滑动变阻器阻值R的变化关系图象如图乙所示,下列说法正确的是( )
在如图所示的电路中,调节滑动变阻器的阻值,电源路端电压U随滑动变阻器阻值R的变化关系图象如图乙所示,下列说法正确的是( )| A. | 当R=4Ω时,电源总功率为16W,内阻热功率为2W | |
| B. | 电源电动势E=6V,内阻r=1Ω | |
| C. | 该电源输出功率的最大值为4.5W | |
| D. | 滑动变阻器阻值从0.5Ω到10Ω逐渐变大过程中,电源的总功率减小,输出功率增大 |
4.对下列四幅图的描述正确的是( )


| A. | 图A可能是机车以恒定功率启动时,速度大小与时间变化的关系图象 | |
| B. | 图B可能是竖直上抛运动的下落阶段速度随时间变化的关系图象 | |
| C. | 图C可能是平抛运动的竖直方向速度随时间变化的关系图象 | |
| D. | 图D可能是匀速圆周运动的向心力大小随时间变化的关系图象 |
 如图所示,截面为半圆形的透明圆柱体其折射率为n,圆心为O点,半圆柱体的圆弧部分外表面涂上水银层,可将光线在圆柱面的内表面全部反射.现有一束细光线从直径AB上的M点以入射角θ射入圆柱体的AB界面,经球面反射后恰好在AB界面上的N点发生全反射,设MO长为l1,ON长为l2,求:$\frac{{l}_{1}}{{l}_{2}}$=?
如图所示,截面为半圆形的透明圆柱体其折射率为n,圆心为O点,半圆柱体的圆弧部分外表面涂上水银层,可将光线在圆柱面的内表面全部反射.现有一束细光线从直径AB上的M点以入射角θ射入圆柱体的AB界面,经球面反射后恰好在AB界面上的N点发生全反射,设MO长为l1,ON长为l2,求:$\frac{{l}_{1}}{{l}_{2}}$=? 如图所示,OAC的半径为l,圆心角为120°的扇形金属框,O点为圆心,OA边与OC边电阻不计,圆弧AC单位长度的电阻相等,总阻值为4r,长度也为l,电阻为r的金属秆OD绕点O从OA位置以角速度ω顺时针匀速转动,整个过程中金属秆两端与金属框接触良好,求金属秆OD转过60°时它两端的电压U的大小.
如图所示,OAC的半径为l,圆心角为120°的扇形金属框,O点为圆心,OA边与OC边电阻不计,圆弧AC单位长度的电阻相等,总阻值为4r,长度也为l,电阻为r的金属秆OD绕点O从OA位置以角速度ω顺时针匀速转动,整个过程中金属秆两端与金属框接触良好,求金属秆OD转过60°时它两端的电压U的大小. 如图所示,间距L=20cm的光滑水平导轨上垂直于导轨放着一金属棒,金属棒的电阻为r=0.5Ω,质量m=2kg,导轨左端的定值电阻R=0.5Ω,导轨电阻不计,匀强磁场垂直于导轨平面,磁感应强度为5T.金属棒在一个F=20N的水平拉力作用下由静止开始向右运动,当金属棒的速度v=10m/s时,棒向右运动的距离S=6m,请问:
如图所示,间距L=20cm的光滑水平导轨上垂直于导轨放着一金属棒,金属棒的电阻为r=0.5Ω,质量m=2kg,导轨左端的定值电阻R=0.5Ω,导轨电阻不计,匀强磁场垂直于导轨平面,磁感应强度为5T.金属棒在一个F=20N的水平拉力作用下由静止开始向右运动,当金属棒的速度v=10m/s时,棒向右运动的距离S=6m,请问: 如图所示,匀强磁场的磁感应强度为0.4T,R=100Ω,C=100μF,ab长20cm,当ab以v=10m/s的速度向右匀速运动时,电容器上极板带正电,下极板带负电,带电量为8×10-5C.
如图所示,匀强磁场的磁感应强度为0.4T,R=100Ω,C=100μF,ab长20cm,当ab以v=10m/s的速度向右匀速运动时,电容器上极板带正电,下极板带负电,带电量为8×10-5C.