题目内容
5. 如图,用一块长L1=1m的木板在墙和桌面间架设斜面,桌面长L2=1.5m.斜面与水平桌面的倾角θ可在0~60°间调节后固定.将小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.2,忽略物块在斜面与桌面交接处的能量损失.重力加速度取10m/s2.求:
如图,用一块长L1=1m的木板在墙和桌面间架设斜面,桌面长L2=1.5m.斜面与水平桌面的倾角θ可在0~60°间调节后固定.将小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.2,忽略物块在斜面与桌面交接处的能量损失.重力加速度取10m/s2.求:(1)在图上画出物块在斜面上的受力分析图;
(2)求θ角增大到多少时,物块能从斜面开始下滑;
(3)当θ增大到30°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2.
分析 (1)分析物块的受力情况:重力、斜面的支持力和摩擦力,再画出受力分析图;
(2)当物块所受的静摩擦力恰好达到最大值时,物块开始沿斜面下滑,根据共点力平衡求出物体能沿斜面开始下滑时斜面的倾角.
(2)对全过程运用动能定理,求出物块与桌面间的动摩擦因数μ2.
解答 解:(1)物块在斜面上的受力分析图如下图所示.
(2)当物块所受的静摩擦力恰好达到最大值时,物块开始沿斜面下滑,此时摩擦力大小为 f=μ1N=μ1mgcosθ;
由平衡条件有 mgsinθ=f
联立解得 μ1=tanθ
得 θ=arctan$\frac{1}{5}$
所以θ角增大到arctan$\frac{1}{5}$时,物块能从斜面开始下滑.
(3)当θ增大到30°时,物块恰能停在桌面边缘时,对全过程运用动能定理得:
mgL1sin30°-μ1mgcos30°•L1-μ2mg(L2-L1cos30°)=0-0,
代入数据解得 μ2=$\frac{6+\sqrt{3}}{15}$≈0.515.
答:
(1)在图上画出物块在斜面上的受力分析图如图;
(2)θ角增大到arctan$\frac{1}{5}$时,物块能从斜面开始下滑;
(3)当θ增大到30°时,物块恰能停在桌面边缘,物块与桌面间的动摩擦因数μ2是0.515.
点评 本题考查了共点力平衡和动能定理的综合运用,对于第三问,也可以运用动力学知识求解,但是没有动能定理处理简洁.

练习册系列答案
相关题目
15. 如图所示,一理想变压器的原、副线圈的匝数比为2:1,在原、副线圈的回路中分别接有阻值相同的电阻R,原线圈一侧接在电压为220V的正弦交流电源上,不计一切导线电阻.设副线圈回路中电阻两端的电压为U,原、副线圈回路中电阻R消耗功率的比值为k,则( )
如图所示,一理想变压器的原、副线圈的匝数比为2:1,在原、副线圈的回路中分别接有阻值相同的电阻R,原线圈一侧接在电压为220V的正弦交流电源上,不计一切导线电阻.设副线圈回路中电阻两端的电压为U,原、副线圈回路中电阻R消耗功率的比值为k,则( )
 如图所示,一理想变压器的原、副线圈的匝数比为2:1,在原、副线圈的回路中分别接有阻值相同的电阻R,原线圈一侧接在电压为220V的正弦交流电源上,不计一切导线电阻.设副线圈回路中电阻两端的电压为U,原、副线圈回路中电阻R消耗功率的比值为k,则( )
如图所示,一理想变压器的原、副线圈的匝数比为2:1,在原、副线圈的回路中分别接有阻值相同的电阻R,原线圈一侧接在电压为220V的正弦交流电源上,不计一切导线电阻.设副线圈回路中电阻两端的电压为U,原、副线圈回路中电阻R消耗功率的比值为k,则( )| A. | U=66V,k=$\frac{1}{9}$ | B. | U=22V,k=$\frac{1}{9}$ | C. | U=110V,k=$\frac{1}{4}$ | D. | U=88V,k=$\frac{1}{4}$ |
16. 如图所示,水平放置的平行板电容器的两板间有一竖直向上的匀强电场,下板接地,两板间距离为10cm,A点距下板3cm,B点距上板3cm.质量m=0.01kg、电荷量为+10-3C的小球能够在A点保持静止.现将小球移到匀强电场之外.下列说法正确的是( )
如图所示,水平放置的平行板电容器的两板间有一竖直向上的匀强电场,下板接地,两板间距离为10cm,A点距下板3cm,B点距上板3cm.质量m=0.01kg、电荷量为+10-3C的小球能够在A点保持静止.现将小球移到匀强电场之外.下列说法正确的是( )
 如图所示,水平放置的平行板电容器的两板间有一竖直向上的匀强电场,下板接地,两板间距离为10cm,A点距下板3cm,B点距上板3cm.质量m=0.01kg、电荷量为+10-3C的小球能够在A点保持静止.现将小球移到匀强电场之外.下列说法正确的是( )
如图所示,水平放置的平行板电容器的两板间有一竖直向上的匀强电场,下板接地,两板间距离为10cm,A点距下板3cm,B点距上板3cm.质量m=0.01kg、电荷量为+10-3C的小球能够在A点保持静止.现将小球移到匀强电场之外.下列说法正确的是( )| A. | 上板的电势比下板高10V | |
| B. | A点的电势为3V | |
| C. | 电荷量为-10-3C的带负电的点电荷在A点的电势能为3×10-3J | |
| D. | 将电荷量为-10-3C的带负电的点电荷从A点移到B点,电场力对该点电荷做功4×10-3J |
13. 如图所示,在正点电荷形成的电场中有A、B两点,分别用 φA、φB表示A、B两点的电势,分别用EA、EB表示A、B两点的电场强度,则( )
如图所示,在正点电荷形成的电场中有A、B两点,分别用 φA、φB表示A、B两点的电势,分别用EA、EB表示A、B两点的电场强度,则( )
 如图所示,在正点电荷形成的电场中有A、B两点,分别用 φA、φB表示A、B两点的电势,分别用EA、EB表示A、B两点的电场强度,则( )
如图所示,在正点电荷形成的电场中有A、B两点,分别用 φA、φB表示A、B两点的电势,分别用EA、EB表示A、B两点的电场强度,则( )| A. | φA>φBEA>EB | B. | φA<φB EA<EB | C. | φA>φB EA<EB | D. | φA=φB EA=EB |
10.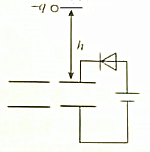 如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )
如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )
 如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )
如图所示,平行板电容器水平放置,电源通过二极管给电容充电,上、下极板正中有一小孔,质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板小孔处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场)( )| A. | 若将上极板稍向上移动,则小球到达下极板小孔处速度恰为零 | |
| B. | 若将上极板稍向下移动,则小球到达下极板小孔处速度恰为零 | |
| C. | 若将下极板稍向上移动,则小球到达下极板小孔前速度就已为零 | |
| D. | 若将上极板稍向下移动,则小球到达下极板小孔处速度仍不为零 |
15. 如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )
如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )
 如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )
如图所示,质量为M,内壁光滑的半球形绝缘容器静止在粗糙水平地面上,O为球心.两个完全相同的小球A、B质量均为m,带有同种电荷,带电量分别为qA、qB,A、B处于静止状态,两球与O的连线与水平面均成30°角,此时容器对A球的弹力为FN1.由于缓慢的漏电,A、B两球缓慢移动,经过时间t,A球与O的连线与水平面成60°角,此时A、B两球的带电量分别为qA′、qB′,容器对A球的弹力为FN2.关于此过程的说法正确的是( )| A. | 地面对容器有水平方向的摩擦力 | B. | FN1:FN2=1:$\sqrt{3}$ | ||
| C. | 地面对容器的弹力小于(M+2m)g | D. | (qAqB):(qA′qB′)=9:1 |
 如图甲所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场方向垂直,已知线圈的匝数N=100,边长ab=1.0m,bc=0.5m,电阻r=2Ω.磁感应强度B随时间变化的规律如图乙所示,取垂直纸面向里为磁场的正方向,求:
如图甲所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场方向垂直,已知线圈的匝数N=100,边长ab=1.0m,bc=0.5m,电阻r=2Ω.磁感应强度B随时间变化的规律如图乙所示,取垂直纸面向里为磁场的正方向,求: 如图所示,分布在半径为R的圆形区域内的匀强磁场,磁感应 强度为B,方向垂直纸面向里.电荷量为负q、质量为m的带电粒子从磁场边缘A点沿圆半径AO方向射入磁场,粒子离开磁场时速度方向偏转了90°角.求:
如图所示,分布在半径为R的圆形区域内的匀强磁场,磁感应 强度为B,方向垂直纸面向里.电荷量为负q、质量为m的带电粒子从磁场边缘A点沿圆半径AO方向射入磁场,粒子离开磁场时速度方向偏转了90°角.求: