题目内容
9．
如图所示，在倾角为θ的光滑坡面上放一块上表面粗糙，下表面光滑的木板，木块质量为ml，质量为m2的人在木板上应向沿斜面向下以加速度$\frac{{m}_{1}gsinθ+{m}_{2}gsinθ}{{m}_{2}}$奔跑时，可使木板不动．
分析 为了使木板与斜面保持相对静止，必须满足木板在斜面上的合力为零，所以人施于木板的摩擦力F应沿斜面向上，故人应加速下跑．现分别对人和木板应用牛顿第二定律即可求解．
解答 解：设此时人与木板间的摩擦力为F，人沿斜面向下运动的加速度为a，现对人和木板分别应用平衡条件和牛顿第二定律有
对木板：m1gsinθ=F
对人：m2gsinθ+F=m2a
联立以上解得：a=$\frac{{m}_{1}gsinθ+{m}_{2}gsinθ}{{m}_{2}}$，方向沿斜面向下
故答案为：沿斜面向下；$\frac{{m}_{1}gsinθ+{m}_{2}gsinθ}{{m}_{2}}$
点评 本题主要考查了牛顿第二定律的直接应用，关键要能根据运动情况分析受力情况，难度适中．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
7．
如图所示，一正方形线圈的匝数为n，边长为a，电阻为R，线圈平面与匀强磁场垂直，且一半处在磁场中．在△t时间内，磁感应强度的方向不变，大小由B均匀地增大到2B．求当磁感应强度增大到2B时，线圈受到的安培力的大小为（ ）
如图所示，一正方形线圈的匝数为n，边长为a，电阻为R，线圈平面与匀强磁场垂直，且一半处在磁场中．在△t时间内，磁感应强度的方向不变，大小由B均匀地增大到2B．求当磁感应强度增大到2B时，线圈受到的安培力的大小为（ ）| A． | $\frac{n{B}^{2}{a}^{3}}{2△tR}$ | B． | $\frac{\sqrt{2}n{B}^{2}{a}^{3}}{△tR}$ | C． | $\frac{n{B}^{2}{a}^{3}}{△tR}$ | D． | $\frac{2n{B}^{2}{a}^{3}}{△tR}$ |
17．一个标有“220V，60W”的电灯泡，当工作电压为110V，它的实际功率（ ）
| A． | 等于15W | B． | 大于15W | C． | 小于15W | D． | 无法确定 |
4．一辆汽车在一段时间内的x-t图象如图所示，由图可知（ ）
| A． | 在0～10s内，汽车做匀加速直线运动 | |
| B． | 汽车在0～10s内的速度比30～40s内的速度大 | |
| C． | 在10～30s内，汽车处于静止状态 | |
| D． | 在10～30s内，汽车做匀速直线运动 |
14．
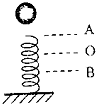如图所示，自由下落的小球下落一段时间后，与轻质弹簧接触，从它接触弹簧开始，到弹簧压缩到最短的过程中，即弹簧上端位置由A→O→B，且弹簧被压缩到O位置时小球所受弹力等于重力，则小球速度最大时，弹簧上端位于（ ）
如图所示，自由下落的小球下落一段时间后，与轻质弹簧接触，从它接触弹簧开始，到弹簧压缩到最短的过程中，即弹簧上端位置由A→O→B，且弹簧被压缩到O位置时小球所受弹力等于重力，则小球速度最大时，弹簧上端位于（ ）| A． | A位置 | B． | B位置 | C． | OB之间某一位置 | D． | O位置 |
1．
如图所示，三块相同的小木块从相同的高度由静止开始同时释放，其中A做自由落体运动，B在自由下落的中途被一水平方向的子弹射入，C在释放的瞬间被一水平方向的子弹射入．则关于它们的下落时间tA、tB、tC的关系，正确的是（ ）
如图所示，三块相同的小木块从相同的高度由静止开始同时释放，其中A做自由落体运动，B在自由下落的中途被一水平方向的子弹射入，C在释放的瞬间被一水平方向的子弹射入．则关于它们的下落时间tA、tB、tC的关系，正确的是（ ）| A． | tA=tB=tC | B． | tA=tB＜tC | C． | tA＜tB＜tC | D． | tA=tC＜tB |
在研究两个共点力合成的实验中得到如图所示的合力F与两个分力的夹角θ的关系图象．求两个分力的大小分别为多少？这两个力的合力的变化范围为多少？
19．
倾斜长木板一端固定在水平轴O上，另一端缓慢放低，放在长木板上的物块m 一直保持相对木板静止状态，如图所示．在这一过程中，物块m受到长木板支持力FN和摩擦力Ff的大小变化情况是（ ）
倾斜长木板一端固定在水平轴O上，另一端缓慢放低，放在长木板上的物块m 一直保持相对木板静止状态，如图所示．在这一过程中，物块m受到长木板支持力FN和摩擦力Ff的大小变化情况是（ ）| A． | FN变大，Ff变大 | B． | FN变小，Ff变小 | C． | FN变大，Ff变小 | D． | FN变小，Ff变大 |