题目内容
10.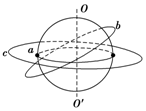 如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )
如图所示,a为赤道上的物体,随地球自转做匀速圆周运动,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球的同步卫星,已知地球半径为R,地球同步卫星轨道半径为6.6R;下列说法中正确的是( )| A. | a和c的向心加速度之比为1:6.6 | B. | b和c的向心加速度之比为6.6:1 | ||
| C. | a的运转周期大于c的运转周期 | D. | b的运转周期大于c的运转周期 |
分析 同步卫星的周期、角速度与地球自转的周期、角速度相等,万有引力提供卫星做圆周运动的需要的向心力,应用向心加速度、牛顿第二定律分析答题.
解答 解:A、a、c做圆周运动的角速度ω相等,向心加速度之比:$\frac{{a}_{a}}{{a}_{c}}$=$\frac{{ω}^{2}{r}_{a}}{{ω}^{2}{r}_{c}}$=$\frac{R}{6.6R}$=$\frac{1}{6.6}$,故A正确;
B、万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=$\frac{GM}{{r}^{2}}$,b、c的向心加速度之比:$\frac{{a}_{b}}{{a}_{c}}$=$\frac{{r}_{c}^{2}}{{r}_{b}^{2}}$=$\frac{(6.6R)^{2}}{{R}^{2}}$=$\frac{6.{6}^{2}}{1}$,故B错误;
C、a做圆周运动的周期等于地球自转周期,c做圆周运动的周期等于地球自转周期,a、c的周期相等,故C错误;
D、万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,由于b的轨道半径小于c的轨道半径,则b的周期小于c的周期,故D错误;
故选:A.
点评 本题考查了万有引力定律的应用,知道同步卫星的周期等于地球自转周期、知道万有引力提供向心力是解题的前提与关键,应用万有引力公式与牛顿第二定律即可解题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
1.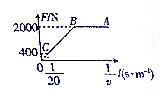 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )| A. | 在AB过程中,电动车做匀加速运动 | |
| B. | 在整个过程中,电动车受到的阻力为2000N | |
| C. | 在整个过程中,电动车发动机的最大功率为8000W | |
| D. | 在整个过程中,电动车克服阻力做的功为72000J |
18.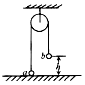 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )| A. | $\frac{m}{M+m}$h | B. | $\frac{M}{M+m}$h | C. | $\frac{2m}{M+m}$h | D. | $\frac{2M}{M+m}$h |
20.关于力和运动,下列说法中正确的是( )
| A. | 如果物体运动,它一定受到力的作用 | |
| B. | 力是使物体做变速运动的原因 | |
| C. | 力是使物体产生加速度的原因 | |
| D. | 力只能改变速度的大小 |

 如图所示,载货车厢通过悬臂固定在缆绳上,缆绳与水平方向夹角为θ,当缆绳带动车厢以加速度a匀加速向上运动时,货物在车厢中与车厢相对静止,假设滑动摩擦力等于最大静摩擦力,并求货物与车厢的动摩擦因数至少为$\frac{acosθ}{g+asinθ}$.
如图所示,载货车厢通过悬臂固定在缆绳上,缆绳与水平方向夹角为θ,当缆绳带动车厢以加速度a匀加速向上运动时,货物在车厢中与车厢相对静止,假设滑动摩擦力等于最大静摩擦力,并求货物与车厢的动摩擦因数至少为$\frac{acosθ}{g+asinθ}$.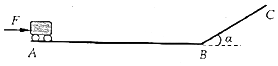 如图所示,长为L的水平面AB与倾角α=30°的斜面BC在B点平滑连接,水平面上质量为m的小推车从A处由静止开始,在沿水平方向的恒定推力F作用下运动.当小推车通过B点后撤去推力,靠惯性滑行到达斜面顶端时速度刚好减为零.已知小推车与水平面和斜面间的动摩擦因数均为μ,重力加速度大小为g,求:
如图所示,长为L的水平面AB与倾角α=30°的斜面BC在B点平滑连接,水平面上质量为m的小推车从A处由静止开始,在沿水平方向的恒定推力F作用下运动.当小推车通过B点后撤去推力,靠惯性滑行到达斜面顶端时速度刚好减为零.已知小推车与水平面和斜面间的动摩擦因数均为μ,重力加速度大小为g,求: 为如图所示,一空心小容器A内装高压气体,总质量为MA=3m,将容器A放在质量为M车=2m的长平板车ac左端a点,平板车上表面ab段光滑,bc段粗糙,bc=L,整个装置静止在光滑水平面上.现打开容器A的阀门向外喷射气体使A向右运动,喷气过程所经历的时间为t,喷出气体的质量为m,喷射气体的对地速度始终为v,容器A到达b点前已停止向外喷气,最后容器A恰好到达平板车右端c点与平板车一起向右运动.求:
为如图所示,一空心小容器A内装高压气体,总质量为MA=3m,将容器A放在质量为M车=2m的长平板车ac左端a点,平板车上表面ab段光滑,bc段粗糙,bc=L,整个装置静止在光滑水平面上.现打开容器A的阀门向外喷射气体使A向右运动,喷气过程所经历的时间为t,喷出气体的质量为m,喷射气体的对地速度始终为v,容器A到达b点前已停止向外喷气,最后容器A恰好到达平板车右端c点与平板车一起向右运动.求: 如图,设想光滑水平面上有两同样大小的小球,质量为m1的小球A以v1速度向右作匀速直线运动,与质量为m2的静止小球B发生碰撞,碰后小球A速度变为v1′,小球B速度变为v2′,方向均向右,若规定向右为正方向.试分析:
如图,设想光滑水平面上有两同样大小的小球,质量为m1的小球A以v1速度向右作匀速直线运动,与质量为m2的静止小球B发生碰撞,碰后小球A速度变为v1′,小球B速度变为v2′,方向均向右,若规定向右为正方向.试分析: