题目内容
1. 如图所示,固定于水平面上、倾角θ=37°的光滑斜面底端固定一与斜面偏小的轻弹簧,劲度系数k=40N/m.将一质量为m=0.2kg的物块(可视为质点),放置在质量M=0.8kg的木板上,木板和物块一起自斜面顶端由静止释放.当木板的下端到达A点时,弹簧的压缩量x1=0.1m,木板正处在加速下滑的过程中,速度v0=1m/s,此时物块刚好相对木板开始滑动;木板继续向下运动,其下端到达B点时,木板处于平衡状态,物块恰好将滑离木板(滑离后物块未触及弹簧和斜面).设物块与木板间的最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,固定于水平面上、倾角θ=37°的光滑斜面底端固定一与斜面偏小的轻弹簧,劲度系数k=40N/m.将一质量为m=0.2kg的物块(可视为质点),放置在质量M=0.8kg的木板上,木板和物块一起自斜面顶端由静止释放.当木板的下端到达A点时,弹簧的压缩量x1=0.1m,木板正处在加速下滑的过程中,速度v0=1m/s,此时物块刚好相对木板开始滑动;木板继续向下运动,其下端到达B点时,木板处于平衡状态,物块恰好将滑离木板(滑离后物块未触及弹簧和斜面).设物块与木板间的最大静摩擦力等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:(1)木板下端首次到达A点时,木板的加速度a的大小.
(2)物块与木板间的动摩擦因数μ;
(3)木板下端再次返回到A点时,木板的速度v0.(结果可保留根号)
分析 (1)对整体进行分析,根据牛顿第二定律可求得加速度大小;
(2)对m分析,根据牛顿第二定律可求得动摩擦因数;
(3)B点处对M分析,根据平衡条件可求得位移关系,再对运动过程根据动能定理列式,联立即可求得木板的速度v0.
解答 解:(1)木板下端首次到达A点时,对M、m,由牛顿第二定律得:
(M+m)gsinθ-kx1=(M+m)a
代入数据解得:
a=2m/s2;
(2)对m,由牛顿第二定律有:
mgsinθ-μmgcosθ=ma
代入数据解得:μ=0.5;
(3)在B点,对M,由平衡条件可得:
mgsinθ+μmgcosθ=kx2
木板下端由A运动到B的过程中,木板的位移△x=x2-x1
木板下端两次经过A点的过程中
对M,由动能定理可得:
μmgcosθ•△x=$\frac{1}{2}$Mv2-$\frac{1}{2}$Mv02
解得:v=$\frac{3\sqrt{3}}{5}$m/s;
答:(1)木板下端首次到达A点时,木板的加速度a的大小为2m/s2;
(2)物块与木板间的动摩擦因数μ为0.5;
(3)木板下端再次返回到A点时,木板的速度v0为$\frac{3\sqrt{3}}{5}$m/s;
点评 本题综合考查了动能定理、牛顿第二定律以及共点力平衡条件的应用,要注意正确分析物理过程,正确受力分析,再正确选择物理规律求解即可.

练习册系列答案
相关题目
7. 如图所示,两颗靠得较近的天体叫双星,它们以两者重心连线上的某点为圆心做匀速圆周运动,因而不至于因引力作用而吸引在一起,以下关于双星的说法中不正确的是( )
如图所示,两颗靠得较近的天体叫双星,它们以两者重心连线上的某点为圆心做匀速圆周运动,因而不至于因引力作用而吸引在一起,以下关于双星的说法中不正确的是( )
 如图所示,两颗靠得较近的天体叫双星,它们以两者重心连线上的某点为圆心做匀速圆周运动,因而不至于因引力作用而吸引在一起,以下关于双星的说法中不正确的是( )
如图所示,两颗靠得较近的天体叫双星,它们以两者重心连线上的某点为圆心做匀速圆周运动,因而不至于因引力作用而吸引在一起,以下关于双星的说法中不正确的是( )| A. | 它们做圆周运动的角速度$\frac{{ω}_{1}}{{ω}_{2}}$=$\frac{{m}_{2}}{{m}_{1}}$ | |
| B. | 它们做圆周运动的线速度$\frac{{v}_{1}}{{v}_{2}}$=$\frac{{m}_{2}}{{m}_{1}}$ | |
| C. | 它们做圆周运动的向心力大小相等 | |
| D. | 它们做圆周运动的半径$\frac{{r}_{1}}{{r}_{2}}$=$\frac{{m}_{2}}{{m}_{1}}$ |
14.蹦床是一种特具观赏性的奥运比赛项目,图甲中一质量为m的运动员正在进行训练,设运动员仅在竖直方向上运动,运动员的脚在接触蹦床过程中,蹦床对运动员的弹力F随时间的变化规律可通过传感器用计算机绘制出来,如图乙所示.则对t2一t4过程,以下说法正确的是( )


| A. | 蹦床的弹性势能转化为运动员的动能 | |
| B. | 蹦床的弹性势能转化为运动员的重力势能 | |
| C. | 运动员的动能不断增大 | |
| D. | 运动员的动能先增大后减小 |
6. 如图所示,一理想变压器原线圈匝数n1=500匝,副线圈匝数n2=100匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V)副线圈中接一电动机内阻为10Ω,电流表A2示数为1A.电表对电路的影响忽略不计,则下列说法正确的是( )
如图所示,一理想变压器原线圈匝数n1=500匝,副线圈匝数n2=100匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V)副线圈中接一电动机内阻为10Ω,电流表A2示数为1A.电表对电路的影响忽略不计,则下列说法正确的是( )
 如图所示,一理想变压器原线圈匝数n1=500匝,副线圈匝数n2=100匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V)副线圈中接一电动机内阻为10Ω,电流表A2示数为1A.电表对电路的影响忽略不计,则下列说法正确的是( )
如图所示,一理想变压器原线圈匝数n1=500匝,副线圈匝数n2=100匝,原线圈中接一交变电源,交变电源电压u=220$\sqrt{2}$sin100πt(V)副线圈中接一电动机内阻为10Ω,电流表A2示数为1A.电表对电路的影响忽略不计,则下列说法正确的是( )| A. | 此交流电的频率为100Hz | |
| B. | 此电动机输出功率为44W | |
| C. | 电流表A1示数为0.2A | |
| D. | 如果电动机被卡住而不损坏,则电源的输出功率变为原来的4.4倍 |
10. 欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.
欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.
问:(1)通过实验,欣欣发现灯泡的电阻是变化(填“不变”“变化”)的,这是因为随电流的减小灯丝温度降低,而使电阻阻值减小.
(2)强强也对欣欣的实验进行了研究,发现欣欣记录的数据中有一个电流值有错误,这个错误数据是0.20,请简要讲出你的判断依据.
(3)当电流为0.50A时,电阻箱两端的电压是多少?
(4)灯泡的铭牌上不清楚的数字是多少?(写出计算过程)
 欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.
欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.| 电流/A | 0.90 | 0.80 | 0.50 | 0.36 | 0.28 | 0.20 |
| 电阻/Ω | 8 | 10 | 20 | 30 | 40 | 50 |
(2)强强也对欣欣的实验进行了研究,发现欣欣记录的数据中有一个电流值有错误,这个错误数据是0.20,请简要讲出你的判断依据.
(3)当电流为0.50A时,电阻箱两端的电压是多少?
(4)灯泡的铭牌上不清楚的数字是多少?(写出计算过程)
11.在图示的闭合电路中,当滑片P向右移动时,两电表读数的变化不正确的是( )


| A. |  变大, 变大, 变大 变大 | B. |  变小, 变小, 变大 变大 | C. |  变大, 变大, 变小 变小 | D. |  变小, 变小, 变小 变小 |
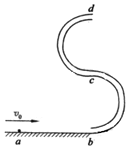 如图所示的“s”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道在水平方向不可移动.弹射装置将一个小球(小球的直径略小于细圆管内径)从a点沿水平地面向b点运动并进入轨道,经过轨道后从最高点d水平抛出.已知小球与地面ab段间的动摩擦因数为μ,ab段长L,圆的半径R,小球质量m,求:
如图所示的“s”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道在水平方向不可移动.弹射装置将一个小球(小球的直径略小于细圆管内径)从a点沿水平地面向b点运动并进入轨道,经过轨道后从最高点d水平抛出.已知小球与地面ab段间的动摩擦因数为μ,ab段长L,圆的半径R,小球质量m,求: 如图所示,在绝缘水平面上的O点固定一正电荷,电荷量为Q,在离O点高度为r0的A处由静止释放一个带同种电荷、电荷量为q的液珠,液珠开始运动瞬间的加速度大小恰好为重力加速度g,沿竖直方向运动到距O点距离为2r0的B点(图中未画出)时,液珠的速度刚好为零.已知静电常量为k,两电荷均可看成点电荷,不计空气阻力.
如图所示,在绝缘水平面上的O点固定一正电荷,电荷量为Q,在离O点高度为r0的A处由静止释放一个带同种电荷、电荷量为q的液珠,液珠开始运动瞬间的加速度大小恰好为重力加速度g,沿竖直方向运动到距O点距离为2r0的B点(图中未画出)时,液珠的速度刚好为零.已知静电常量为k,两电荷均可看成点电荷,不计空气阻力.