题目内容
2. 如图所示,趣味运动会上运动员手持球拍托着乒乓球向前跑,球拍与水平方向的夹角为θ,运动员先以a=$\frac{10}{3}$m/s2匀加速向前跑,然后以速度v=8m/s匀速向前跑,不计球与拍之间的摩擦,球与拍始终保持相对静止,设跑动过程中空气对球的作用力水平且大小恒为f=0.1N,球的质量为m=0.01kg.重力加速度g取10m/s2,求:
如图所示,趣味运动会上运动员手持球拍托着乒乓球向前跑,球拍与水平方向的夹角为θ,运动员先以a=$\frac{10}{3}$m/s2匀加速向前跑,然后以速度v=8m/s匀速向前跑,不计球与拍之间的摩擦,球与拍始终保持相对静止,设跑动过程中空气对球的作用力水平且大小恒为f=0.1N,球的质量为m=0.01kg.重力加速度g取10m/s2,求:(1)匀速运动时,球拍与水平方向的夹角θ的大小;
(2)匀加速运动时,球拍与水平方向的夹角θ的大小(可用三角函数表示 ).
分析 (1)匀速运动时,对乒乓球进行受力分析,受重力、支持力和阻力,根据平衡条件求解,球拍与水平方向的夹角θ
(2)匀加速运动时,根据牛顿第二定律列出水平和竖直方向的分量式求解
解答  解(1)以乒乓球为研究对象,对乒乓球进行受力分析,乒乓球受到重力、支持力和阻力,受力如图所示,根据平衡条件有:
解(1)以乒乓球为研究对象,对乒乓球进行受力分析,乒乓球受到重力、支持力和阻力,受力如图所示,根据平衡条件有:
$tanθ=\frac{f}{mg}=\frac{0.1}{0.01×10}=1$…①
由①知θ=45°
(2)小球受力分析如(1)题图
由牛顿第二定律得:
水平方向上:${F}_{N}^{\;}sinθ-f=ma②$
竖直方向:上${F}_{N}^{\;}cosθ=mg③$
②③联立得:$tanθ=\frac{5}{3}$
答:(1)匀速运动时,球拍与水平方向的夹角为45°
(2)匀加速运动时,球拍与水平方向的夹角θ的正切值$tanθ=\frac{5}{3}$
点评 解决本题的关键是正确进行受力分析,画受力分析图,根据牛顿第二定律列式求解.

练习册系列答案
相关题目
12. 在云南省某地方到现在还要依靠滑铁索过江,若把这滑铁索过江简化成如图所示的模型,铁索的两个固定点A、B在同一水平面内,AB间的距离为L=80m,铁索的最低点离AB连线的垂直距离为H=8m,若把绳索看做是圆弧,已知一质量m=52kg的人借助滑轮(滑轮质量不计)滑到最低点的速度为10m/s,那么( )
在云南省某地方到现在还要依靠滑铁索过江,若把这滑铁索过江简化成如图所示的模型,铁索的两个固定点A、B在同一水平面内,AB间的距离为L=80m,铁索的最低点离AB连线的垂直距离为H=8m,若把绳索看做是圆弧,已知一质量m=52kg的人借助滑轮(滑轮质量不计)滑到最低点的速度为10m/s,那么( )
 在云南省某地方到现在还要依靠滑铁索过江,若把这滑铁索过江简化成如图所示的模型,铁索的两个固定点A、B在同一水平面内,AB间的距离为L=80m,铁索的最低点离AB连线的垂直距离为H=8m,若把绳索看做是圆弧,已知一质量m=52kg的人借助滑轮(滑轮质量不计)滑到最低点的速度为10m/s,那么( )
在云南省某地方到现在还要依靠滑铁索过江,若把这滑铁索过江简化成如图所示的模型,铁索的两个固定点A、B在同一水平面内,AB间的距离为L=80m,铁索的最低点离AB连线的垂直距离为H=8m,若把绳索看做是圆弧,已知一质量m=52kg的人借助滑轮(滑轮质量不计)滑到最低点的速度为10m/s,那么( )| A. | 人在整个绳索上运动可看成是匀速圆周运动 | |
| B. | 可求得绳索的圆弧半径为100m | |
| C. | 人在滑到最低点时,滑轮对绳索的压力为570N | |
| D. | 人在滑到最低点时,滑轮对绳索的压力为50N |
13. 如图所示,物体在恒力F作用下沿曲线从A运动到B,这时突然使他所受合力的方向反向而大小不变,此后物体运动情况可能是( )
如图所示,物体在恒力F作用下沿曲线从A运动到B,这时突然使他所受合力的方向反向而大小不变,此后物体运动情况可能是( )
 如图所示,物体在恒力F作用下沿曲线从A运动到B,这时突然使他所受合力的方向反向而大小不变,此后物体运动情况可能是( )
如图所示,物体在恒力F作用下沿曲线从A运动到B,这时突然使他所受合力的方向反向而大小不变,此后物体运动情况可能是( )| A. | 物体可能沿曲线Ba运动 | B. | 物体可能沿直线Bb运动 | ||
| C. | 物体可能沿曲线Bc运动 | D. | 物体可能沿原曲线由B返回A |
10.平抛一物体,当抛出1s后它的速度方向与水平方向成45°角,落地时的速度方向与水平方向成60°角,则下列说法错误的是( )
| A. | 初速度为10m/s | B. | 落地速度15m/s | ||
| C. | 开始抛出时距地面的高度20 m | D. | 水平射程10m |
2. 氢原子能级如图所示,已知可见光的光子能量在1.62eV到3.11eV之间,当氢原子从n=3跃迁到n=2的能级时,辐射光的波长为656nm.以下判断正确的是( )
氢原子能级如图所示,已知可见光的光子能量在1.62eV到3.11eV之间,当氢原子从n=3跃迁到n=2的能级时,辐射光的波长为656nm.以下判断正确的是( )
E.处于n=3能级的氢原子吸收1.51ev的能量会发生电离.
 氢原子能级如图所示,已知可见光的光子能量在1.62eV到3.11eV之间,当氢原子从n=3跃迁到n=2的能级时,辐射光的波长为656nm.以下判断正确的是( )
氢原子能级如图所示,已知可见光的光子能量在1.62eV到3.11eV之间,当氢原子从n=3跃迁到n=2的能级时,辐射光的波长为656nm.以下判断正确的是( )E.处于n=3能级的氢原子吸收1.51ev的能量会发生电离.
| A. | 氢原子从n=3能级向n=2能级跃迁时发出的光为可见光 | |
| B. | 用波长为502nm的光照射,能使氢原子从n=2跃迁到n=3的能级 | |
| C. | 氢原子从n=2跃迁到n=1的能级时,辐射光的波长大于656nm | |
| D. | 一群处于n=3能级上的氢原子向低能级跃迁时最多产生3种谱线 | |
| E. | 处于n=3能级的氢原子吸收1.51ev的能量会发生电离 |
19.利用如图1所示的装置研究平抛运动的规律

(1)下列关于该实验的说法正确的是AC.
A.钢球每次从同一位置释放,这样保证钢球每次抛出的初速度相同
B.在实验中设法描出钢球轨迹上的多个点,然后用折线连接就可以得到平抛运动的轨迹
C.实验中必须要求斜槽末端水平
D.该实验产生误差主要是因为斜槽粗糙
(2)某同学在做“研究抛物体的运动”的实验时,让小球多次从斜槽上滚下,在坐标纸上依次记下小球的位置如图2所示(O为小球的抛出点).
a、在图中描出小球的运动轨迹.
b、从图中可看出,某一点的位置有明显的错误,其产生的原因可能是该次实验中,小球从斜槽上滚下时的初始位置比其他几次的位置偏低(填“高”或“低”).
(3)某同学从图象中测得的三组数据如下表所示,则此小球做平抛运动的初速度v0=1.0 m/s.

(1)下列关于该实验的说法正确的是AC.
A.钢球每次从同一位置释放,这样保证钢球每次抛出的初速度相同
B.在实验中设法描出钢球轨迹上的多个点,然后用折线连接就可以得到平抛运动的轨迹
C.实验中必须要求斜槽末端水平
D.该实验产生误差主要是因为斜槽粗糙
(2)某同学在做“研究抛物体的运动”的实验时,让小球多次从斜槽上滚下,在坐标纸上依次记下小球的位置如图2所示(O为小球的抛出点).
a、在图中描出小球的运动轨迹.
b、从图中可看出,某一点的位置有明显的错误,其产生的原因可能是该次实验中,小球从斜槽上滚下时的初始位置比其他几次的位置偏低(填“高”或“低”).
(3)某同学从图象中测得的三组数据如下表所示,则此小球做平抛运动的初速度v0=1.0 m/s.
| x(cm) | 10.00 | 20.00 | 30.00 |
| y(cm) | 5.00 | 20.00 | 45.00 |
20. 如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电量为q,小球可在棒上滑动,小球与棒的动摩擦因数为μ.现将此棒竖直放入沿水平方向的且互相垂直的匀强磁场和匀强电场中,设小球电量不变,电场强度为E,方向水平向右,磁感应强度为B,方向垂直纸面向外,小球沿棒由静止开始下滑,则( )
如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电量为q,小球可在棒上滑动,小球与棒的动摩擦因数为μ.现将此棒竖直放入沿水平方向的且互相垂直的匀强磁场和匀强电场中,设小球电量不变,电场强度为E,方向水平向右,磁感应强度为B,方向垂直纸面向外,小球沿棒由静止开始下滑,则( )
 如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电量为q,小球可在棒上滑动,小球与棒的动摩擦因数为μ.现将此棒竖直放入沿水平方向的且互相垂直的匀强磁场和匀强电场中,设小球电量不变,电场强度为E,方向水平向右,磁感应强度为B,方向垂直纸面向外,小球沿棒由静止开始下滑,则( )
如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电量为q,小球可在棒上滑动,小球与棒的动摩擦因数为μ.现将此棒竖直放入沿水平方向的且互相垂直的匀强磁场和匀强电场中,设小球电量不变,电场强度为E,方向水平向右,磁感应强度为B,方向垂直纸面向外,小球沿棒由静止开始下滑,则( )| A. | 小球先匀加速运动,后匀速运动 | B. | 小球加速度先增大,后减小 | ||
| C. | 小球下落的最大加速度是g | D. | 小球下落的最大速度是$\frac{mg}{qBμ}+\frac{E}{B}$ |
 如图所示,两块水平放置的金属板间距离为d,用导线与一个n匝的线圈连接,线圈置于方向竖直向上的磁场B中,两板间有一个质量为m,电量为+q的油滴恰好处于平衡状态,重力加速度为g,则线圈中的磁场B正在减弱(填“增强”或“减弱”),磁通量变化率为$\frac{mgd}{nq}$.
如图所示,两块水平放置的金属板间距离为d,用导线与一个n匝的线圈连接,线圈置于方向竖直向上的磁场B中,两板间有一个质量为m,电量为+q的油滴恰好处于平衡状态,重力加速度为g,则线圈中的磁场B正在减弱(填“增强”或“减弱”),磁通量变化率为$\frac{mgd}{nq}$.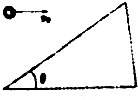 小球以初速度v0正对着倾角为θ的斜面水平抛出,小球恰好垂直撞上斜面.
小球以初速度v0正对着倾角为θ的斜面水平抛出,小球恰好垂直撞上斜面.