题目内容
10．
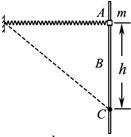如图所示，轻质弹簧一端固定，另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连，弹簧水平且处于原长．圆环从A处由静止开始下滑，经过B处的速度最大（B为杆AC中某一点），到达C处的速度为零，AC=h．如果圆环在C处获得一竖直向上的速度v，恰好能回到A．弹簧始终在弹性限度内，重力加速度为g．则圆环（ ）| A． | 下滑过程中，加速度一直减小 | |
| B． | 下滑过程中，克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| C． | 从A下滑到C过程中弹簧的弹性势能增加量等于mgh | |
| D． | 在C处，弹簧的弹性势能为$\frac{1}{4}$mv2-mgh |
分析 根据圆环的运动情况分析下滑过程中，加速度的变化；研究圆环从A处由静止开始下滑到C和在C处获得一竖直向上的速度v，恰好能回到A两个过程，运用动能定理列出等式求解．
解答 解：A、圆环从A处由静止开始下滑，经过B处的速度最大，到达C处的速度为零，所以圆环先做加速运动，再做减速运动，经过B处的速度最大，所以经过B处的加速度为零，所以加速度先减小，后增大，故A错误；
B、研究圆环从A处由静止开始下滑到C过程，运用动能定理列出等式
mgh-Wf-W弹=0-0=0
在C处获得一竖直向上的速度v，恰好能回到A，运用动能定理列出等式
-mgh+W弹-Wf=0-$\frac{1}{2}$mv2
解得：Wf=-$\frac{1}{4}$mv2，则克服摩擦力做的功为$\frac{1}{4}$mv2，故B正确；
C、由B中的公式得：W弹=$\frac{1}{4}$mv2-mgh，所以在C处，弹簧的弹性势能为mgh-$\frac{1}{4}$mv2，则从A下滑到C过程中弹簧的弹性势能增加量等于mgh-$\frac{1}{4}$mv2，故CD错误．
故选：B
点评 能正确分析小球的受力情况和运动情况，对物理过程进行受力、运动、做功分析，是解决问题的根本方法，掌握动能定理的应用．
练习册系列答案
名校课堂系列答案
相关题目
12．
如图所示是某物体做直线运动的v-t图象，由该图角可知，在0-4s的时间内（ ）
如图所示是某物体做直线运动的v-t图象，由该图角可知，在0-4s的时间内（ ）| A． | 物体做匀加速直线运动 | B． | 物体运动的加速度的大小为5m/s2 | ||
| C． | 1s时物体的速度大小为5m/s | D． | 4s时物体距离出发点最远 |
1．
如图所示为两个不同闭合电路中两个不同电源的U-I图象，O为坐标原点，下列判断正确的是（ ）
如图所示为两个不同闭合电路中两个不同电源的U-I图象，O为坐标原点，下列判断正确的是（ ）| A． | 电动势E1=E2，内阻r1＞r2 | |
| B． | 电动势E1＞E2，内阻r1＞r2 | |
| C． | 电动势E1＜E2，内阻 r1＜r2 | |
| D． | 电动势E1=E2，发生短路时的电流I1＞I2 |
18．某电站到用户的距离为L，在某次输电时，经测量镀电线上的电流为I．为了节省能耗，输电线上损失的电压不能大于U．已知该输电钱的电阻率为ρ，输电线为匀质的导线，则输电线直径的最小值为（ ）
| A． | 2$\sqrt{\frac{2ρLI}{πU}}$ | B． | $\sqrt{\frac{2ρLI}{πU}}$ | C． | 2$\sqrt{\frac{ρLI}{πU}}$ | D． | $\sqrt{\frac{ρLI}{πU}}$ |
5．一定质量的理想气体处于平衡状态Ⅰ，现设法使其温度降低而压强增大，达到平衡状态Ⅱ，则（ ）
| A． | 状态Ⅰ时气体的密度比状态Ⅱ时的大 | |
| B． | 从状态Ⅰ到状态Ⅱ气体对外做功 | |
| C． | 状态Ⅰ时分子间的平均距离比状态Ⅱ时的大 | |
| D． | 状态Ⅰ时每个分子的动能都比状态Ⅱ时的分子平均动能大 |
如图所示，某人在离地面高10m处，以5m/s的初速度水平抛出A球，与此同时在离A球抛出点水平距离s处，另一人竖直上抛B球，不计空气阻力和人的高度，如果要使B球上升到最高点时与A球相遇，则B球的初速度大小为10m/s，B球与A球抛出点的水平距离s为5m．（取g=10m/s2）
如图所示，两个带正电的点电荷M和N，带电量均为Q，固定在光滑绝缘的水平面上，相距2L，A，O，B是MN连线上的三点，且O为中点，OA=OB=$\frac{L}{2}$，一质量为m、电量为q的点电荷以初速度v0从A点出发沿MN连线向N运动，在运动过程中电荷受到大小恒定的阻力作用，但速度为零时，阻力也为零，当它运动到O点时，动能为初动能的n倍，到B点刚好速度为零，然后返回往复运动，直至最后静止．已知静电力恒量为k，取O处电势为零．求：
由某种材料制成的电器元件，其伏安特性曲线如图所示．现将该元件接在电动势为8V，内阻为4Ω的电源两端，通过该元件的电流为1A，该元件消耗的电功率为4W．现将这个元件与一个4Ω的定值电阻串联后接在该电源上，则该元件获得的电功率为1.5W．
某同学利用两物体通过细线连接在定滑轮两边