题目内容
15. 如图所示,某人在离地面高10m处,以5m/s的初速度水平抛出A球,与此同时在离A球抛出点水平距离s处,另一人竖直上抛B球,不计空气阻力和人的高度,如果要使B球上升到最高点时与A球相遇,则B球的初速度大小为10m/s,B球与A球抛出点的水平距离s为5m.(取g=10m/s2)
如图所示,某人在离地面高10m处,以5m/s的初速度水平抛出A球,与此同时在离A球抛出点水平距离s处,另一人竖直上抛B球,不计空气阻力和人的高度,如果要使B球上升到最高点时与A球相遇,则B球的初速度大小为10m/s,B球与A球抛出点的水平距离s为5m.(取g=10m/s2)
分析 根据两球在B球上升到最高点相遇,得出时间的表达式,抓住两球的竖直位移之和等于h求出B的初速度,从而结合速度时间公式求出相遇的时间,根据A球的初速度和时间求出水平距离.
解答 解:两球在B球上升到最高点相遇,则有:t=$\frac{{v}_{B}}{g}$,
A、B两球相遇,在竖直方向上有:$\frac{1}{2}g{t}^{2}+{v}_{B}t-\frac{1}{2}g{t}^{2}=h$,
联立两式解得:vB=10m/s.
运动的时间为:
t=$\frac{{v}_{B}}{g}=\frac{10}{10}s=1s$,
B球与A球抛出点的水平距离为:
s=vAt=5×1m=5m.
故答案为:10;5.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,难度中等.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
6. 近年来,我国一些地区出现了雾霾天气,影响了人们的正常生活.在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方有一辆大卡车正以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.已知小汽车刚刹车时与大卡车相距40m,并开始计时,得到小汽车和大卡车的v-t图象分别如图中a、b所示,以下说法正确的是( )
近年来,我国一些地区出现了雾霾天气,影响了人们的正常生活.在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方有一辆大卡车正以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.已知小汽车刚刹车时与大卡车相距40m,并开始计时,得到小汽车和大卡车的v-t图象分别如图中a、b所示,以下说法正确的是( )
 近年来,我国一些地区出现了雾霾天气,影响了人们的正常生活.在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方有一辆大卡车正以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.已知小汽车刚刹车时与大卡车相距40m,并开始计时,得到小汽车和大卡车的v-t图象分别如图中a、b所示,以下说法正确的是( )
近年来,我国一些地区出现了雾霾天气,影响了人们的正常生活.在一雾霾天,某人驾驶一辆小汽车以30m/s的速度行驶在高速公路上,突然发现正前方有一辆大卡车正以10m/s的速度同方向匀速行驶,小汽车紧急刹车,但刹车过程中刹车失灵.已知小汽车刚刹车时与大卡车相距40m,并开始计时,得到小汽车和大卡车的v-t图象分别如图中a、b所示,以下说法正确的是( )| A. | 由于初始距离太近,即使刹车不失灵也会追尾 | |
| B. | 在t=1s时追尾 | |
| C. | 在t=5s时追尾 | |
| D. | 在t=5s时两车相距最近,但没有追尾 |
3.关于电动势,下列叙述中正确的是( )
| A. | 电源电动势在数值上等于内外电压之和,若外电阻变大,电动势也变大 | |
| B. | 电源电动势等于断路时两极间的电压,电源接入电路时,电动势减小 | |
| C. | 电源的电动势表示电源把其他形式的能转化为电能的本领大小 | |
| D. | 在闭合电路中,并联于电源两端的电压表的示数就是电源电动势 |
10.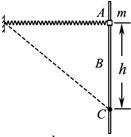 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| C. | 从A下滑到C过程中弹簧的弹性势能增加量等于mgh | |
| D. | 在C处,弹簧的弹性势能为$\frac{1}{4}$mv2-mgh |
7.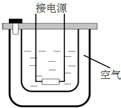 如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )
如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )
 如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )
如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )| A. | 内能保持不变 | B. | 所有分子运动速率都增大 | ||
| C. | 分子势能减小 | D. | 分子平均动能增大 |
4. 某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )
某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )
 某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )
某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )| A. | 第10s末,质点的速度最大 | |
| B. | 在20s内,质点的位移为9m | |
| C. | 第5s末和第15s末,质点的加速度方向相反 | |
| D. | 0~10s内,质点所受合外力的方向与速度方向相反 |
5. 2015年7月的喀山游泳世锦赛中,我省名将陈若琳勇夺女子十米跳台桂冠.她从跳台斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力.下列说法正确的是( )
2015年7月的喀山游泳世锦赛中,我省名将陈若琳勇夺女子十米跳台桂冠.她从跳台斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力.下列说法正确的是( )
 2015年7月的喀山游泳世锦赛中,我省名将陈若琳勇夺女子十米跳台桂冠.她从跳台斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力.下列说法正确的是( )
2015年7月的喀山游泳世锦赛中,我省名将陈若琳勇夺女子十米跳台桂冠.她从跳台斜向上跳起,一段时间后落入水中,如图所示.不计空气阻力.下列说法正确的是( )| A. | 她在空中上升过程中处于超重状态 | |
| B. | 她在空中下落过程中做自由落体运动 | |
| C. | 她即将入水时的速度为整个跳水过程中的最大速度 | |
| D. | 入水过程中,水对她的作用力大小等于她对水的作用力大小 |
 如图所示,水平传送带以速度v=8m/s顺时针匀速转动,现将一质量为m=1kg的小木块轻放在传送带的最左端,木块与传送带间的动摩擦因数μ=0.5.另有一半径为R=0.6m的竖直光滑半圆弧轨道与传送带的最右端B点平滑相接,木块可视为质点,已知木块上半圆轨道通过圆弧的最高点C时对轨道的压力大小等于重力,重力加速度g=10m/s2,求木块在传送带上运动过程中与传送带间因摩擦而产生的内能.
如图所示,水平传送带以速度v=8m/s顺时针匀速转动,现将一质量为m=1kg的小木块轻放在传送带的最左端,木块与传送带间的动摩擦因数μ=0.5.另有一半径为R=0.6m的竖直光滑半圆弧轨道与传送带的最右端B点平滑相接,木块可视为质点,已知木块上半圆轨道通过圆弧的最高点C时对轨道的压力大小等于重力,重力加速度g=10m/s2,求木块在传送带上运动过程中与传送带间因摩擦而产生的内能.