题目内容
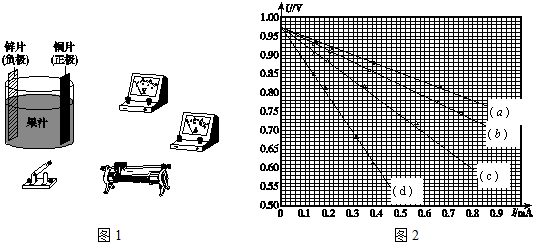
19. 由某种材料制成的电器元件,其伏安特性曲线如图所示.现将该元件接在电动势为8V,内阻为4Ω的电源两端,通过该元件的电流为1A,该元件消耗的电功率为4W.现将这个元件与一个4Ω的定值电阻串联后接在该电源上,则该元件获得的电功率为1.5W.
由某种材料制成的电器元件,其伏安特性曲线如图所示.现将该元件接在电动势为8V,内阻为4Ω的电源两端,通过该元件的电流为1A,该元件消耗的电功率为4W.现将这个元件与一个4Ω的定值电阻串联后接在该电源上,则该元件获得的电功率为1.5W.
分析 在伏安特性曲线上作出电源的外特性曲线,两曲线的交点即为该元件接在电源上的工作状态,由交点读出电压与电流,根据P=UI可求元件的功率.
解答  解:将该元件接在电动势为8V,内阻为4Ω的电源两端,根据闭合电路欧姆定律得:
解:将该元件接在电动势为8V,内阻为4Ω的电源两端,根据闭合电路欧姆定律得:
U=E-Ir,
带入数据得:U=8-4I,
作出电源的外特性曲线,
则两图线交点,即为该元件接在电源上的工作状态,
由图可知,I=1A,U=4V,该元件消耗的电功率为:P=UI=4×1=4W,
将这个元件与一个4Ω的定值电阻串联后接在该电源上,把定值电阻看成电源内阻, 根据闭合电路欧姆定律得:
根据闭合电路欧姆定律得:
U=E-Ir,
带入数据得:U=8-8I,
作出电源的外特性曲线,
由图读出U=2.0V,I=0.75A
则P=UI=1.5W
故答案为:1;4;1.5
点评 本题的技巧是作出电源的外特性曲线,研究交点的意义即可.图象法这是利用数学知识解决物理问题常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.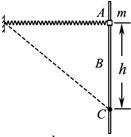 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
 如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )
如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长.圆环从A处由静止开始下滑,经过B处的速度最大(B为杆AC中某一点),到达C处的速度为零,AC=h.如果圆环在C处获得一竖直向上的速度v,恰好能回到A.弹簧始终在弹性限度内,重力加速度为g.则圆环( )| A. | 下滑过程中,加速度一直减小 | |
| B. | 下滑过程中,克服摩擦力做的功为$\frac{1}{4}$mv2 | |
| C. | 从A下滑到C过程中弹簧的弹性势能增加量等于mgh | |
| D. | 在C处,弹簧的弹性势能为$\frac{1}{4}$mv2-mgh |
7.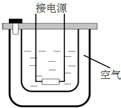 如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )
如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )
 如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )
如图为某实验器材的结构示意图,金属内筒和绝热外筒间封闭了一定体积的理想气体,内筒中有水.在对水加热升温的过程中,被封闭的空气( )| A. | 内能保持不变 | B. | 所有分子运动速率都增大 | ||
| C. | 分子势能减小 | D. | 分子平均动能增大 |
14.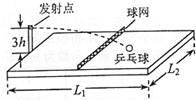 装有乒乓球发射机的球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气阻力,重力加速度为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的取值范围是( )
装有乒乓球发射机的球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气阻力,重力加速度为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的取值范围是( )
 装有乒乓球发射机的球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气阻力,重力加速度为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的取值范围是( )
装有乒乓球发射机的球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气阻力,重力加速度为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的取值范围是( )| A. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{{L}_{1}}^{2}+{{L}_{2}}^{2})g}{6h}}$ | B. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<L1$\sqrt{\frac{g}{6h}}$ | ||
| C. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{{L}_{1}}^{2}+{{L}_{2}}^{2})g}{6h}}$ | D. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<L1$\sqrt{\frac{g}{6h}}$ |
4. 某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )
某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )
 某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )
某一质点沿直线运动的位移x随时间t变化的图象如图所示,则( )| A. | 第10s末,质点的速度最大 | |
| B. | 在20s内,质点的位移为9m | |
| C. | 第5s末和第15s末,质点的加速度方向相反 | |
| D. | 0~10s内,质点所受合外力的方向与速度方向相反 |
8. 一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图,已知O、A的平衡位置相距1.2m,以下判断正确的是( )
一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图,已知O、A的平衡位置相距1.2m,以下判断正确的是( )
 一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图,已知O、A的平衡位置相距1.2m,以下判断正确的是( )
一列简谐横波沿直线传播,以波源O由平衡位置开始振动为计时零点,质点A的振动图象如图,已知O、A的平衡位置相距1.2m,以下判断正确的是( )| A. | 波速为0.6m/s | B. | 波长为2.4m | ||
| C. | 波源起振方向沿y轴负方向 | D. | 质点A的动能在t=4s时为零 |
9. 一列横波在t=0时刻波形如图所示,a、b两质点间距为8m,a、c两质点平衡位置的间距为3m,当t=1s时,质点c恰好通过平衡位置,则波速可能为( )
一列横波在t=0时刻波形如图所示,a、b两质点间距为8m,a、c两质点平衡位置的间距为3m,当t=1s时,质点c恰好通过平衡位置,则波速可能为( )
 一列横波在t=0时刻波形如图所示,a、b两质点间距为8m,a、c两质点平衡位置的间距为3m,当t=1s时,质点c恰好通过平衡位置,则波速可能为( )
一列横波在t=0时刻波形如图所示,a、b两质点间距为8m,a、c两质点平衡位置的间距为3m,当t=1s时,质点c恰好通过平衡位置,则波速可能为( )| A. | 1m/s | B. | 8m/s | C. | 13m/s | D. | 23m/s |
 可见光通信是利用LED灯的光线实现上网的新型高速数据传输技术.如图所示,ABCD是LED闪光灯的圆柱形封装玻璃体,其横截面的直径AB=d,厚度AD=$\frac{\sqrt{3}}{2}$d.LED灯(可视为点光源)固定在玻璃体CD面的圆心O,玻璃体的折射率为$\sqrt{2}$,光在真空中的传播速度为c.求:
可见光通信是利用LED灯的光线实现上网的新型高速数据传输技术.如图所示,ABCD是LED闪光灯的圆柱形封装玻璃体,其横截面的直径AB=d,厚度AD=$\frac{\sqrt{3}}{2}$d.LED灯(可视为点光源)固定在玻璃体CD面的圆心O,玻璃体的折射率为$\sqrt{2}$,光在真空中的传播速度为c.求: