题目内容
6. 如图所示,水平虚线MN下方有一竖直向上的匀强电场,一根轻质绝缘杆(质量不计)两端分别套有A、B两个小球,A球的质量为m,带正电,在匀强电场中受到的电场力为其重力大小的3倍,A球和杆间的滑动摩擦力的大小等于其重力大小.B球的质量为3m,不带电,B球和杆间的滑动摩擦力大小也等于其重力大小,设两球的最大静摩擦力均等于滑动摩擦力,重力加速度为g.开始时A、B球和杆均静止,A球距MN高度为h,同时释放A、B两球和杆,当A球第二次进入电场区域时,A、B两球恰好相遇,运动过程中杆始终保持竖直状态.求:
如图所示,水平虚线MN下方有一竖直向上的匀强电场,一根轻质绝缘杆(质量不计)两端分别套有A、B两个小球,A球的质量为m,带正电,在匀强电场中受到的电场力为其重力大小的3倍,A球和杆间的滑动摩擦力的大小等于其重力大小.B球的质量为3m,不带电,B球和杆间的滑动摩擦力大小也等于其重力大小,设两球的最大静摩擦力均等于滑动摩擦力,重力加速度为g.开始时A、B球和杆均静止,A球距MN高度为h,同时释放A、B两球和杆,当A球第二次进入电场区域时,A、B两球恰好相遇,运动过程中杆始终保持竖直状态.求:(1)A球运动过程中的最大电势能(设MN处电势为零);
(2)从A球第一次进入电场到A球第二次进入电场的过程中经历的时间及杆的长度.
分析 (1)由机械能守恒求出A到达MN时的速度,A进入电场后,由牛顿第二定律求出加速度,由运动学的公式即可求出A在电场中的位移,由电场力做功即可求出电势能的变化;
(2)由△v=a△t求出A的速度减小为0的时间,然后对B进行受力分析,求出B的加速度,由运动学的公式求出B的速度和位移;
此后A向上做加速运动,求出其加速度以及返回MN的时间;重新分析A在MN以上的受力,由牛顿第二定律求出加速度以及向上运动的时间;同理分析B的运动;
A向上到达最高点后再向下运动,结合受力分析,求出对应的时间,再求出B的位移.最后由几何关系求出杆的长度.
解答 解:(1)设A球开始进入电场的速度为v0,根据机械能守恒得:
$4mgh=\frac{1}{2}•4m{v}_{0}^{2}$
所以:${v}_{0}=\sqrt{2gh}$
A球在电场中受到的电场力是重力的3倍,即F=3mg,则A球向下做减速运动,相对于杆向上运动,A球的受力如图1,所以: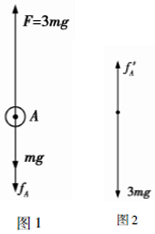
F-mg-fA=maA1
其中:fA=mg
结合已知的条件得:aA1=g方向竖直向上
A球减速到速度等于0的时间:${t}_{1}=\frac{{v}_{0}}{{a}_{A1}}=\sqrt{\frac{2h}{g}}$
向下运动的位移:${x}_{A1}=\frac{{v}_{0}^{2}}{2{a}_{A1}}$
联立得:xA1=h
电场力对A球做负功,W=-Fh=-3mgh
该过程中A的电势能增大,所以A球的最大电势能为3mgh
(2)杆的质量为0,所以杆受到的合力为0,A球对杆有向上的摩擦力,大小为fA=mg,所以B对杆有向下的摩擦力,大小也是mg,小于B与杆之间的最大静摩擦力,所以B与杆相对静止,对B球和杆受力分析如图2,B球和杆一起向下做加速运动,有:
3mg-fA=3maB
联立得:${a}_{B}=\frac{2g}{3}$
在A球的速度减小为0时,B球和杆的速度为:${v}_{B1}={v}_{0}+{a}_{B}{t}_{1}=\frac{5}{3}\sqrt{2gh}$
位移:${x}_{B1}={v}_{0}t+\frac{1}{2}{a}_{B}{t}_{1}^{2}=\frac{8}{3}h$
A球的速度减小为0后向上做匀加速直线运动,仍然受到向上的电场力和向下的摩擦力,所以A的加速度不变,则:aA2=aA1=g
再经过时间t2=${t}_{1}=\sqrt{\frac{2h}{g}}$的时间,A向上以受到v0经过水平线MN,则xA2=h
此过程中B和杆始终向下做匀加速直线运动,加速度不变;
A球向上离开MN时,B的速度:vB2=vB1+aBt2
整理得:${v}_{B2}=\frac{7}{3}\sqrt{2gh}$
向下运动的位移:${x}_{B2}=\frac{({v}_{B1}+{v}_{B2})}{2}•{t}_{2}=4h$
A球向上减速到0的过程中,受到向下的重力和摩擦力的作用,做减速运动,此时:fA+mg=maA3
得:aA3=2g,加速度的方向向下,
A向上减速到0的过程中经历的时间:${t}_{3}=\frac{{v}_{0}}{{a}_{A3}}=\sqrt{\frac{h}{2g}}$
向上运动的位移:${x}_{A3}=\frac{{v}_{0}^{2}}{2{a}_{A3}}=\frac{h}{2}$
A的速度为0时,B和杆的速度:vB3=vB2+aBt3
整理得:${v}_{B3}=\frac{8}{3}\sqrt{2gh}$
向下运动的位移:${x}_{B3}=\frac{({v}_{B2}+{v}_{B3})}{2}•{t}_{3}=\frac{5}{2}h$
A球向上减速为0后受到向下的重力和摩擦力的作用,做加速运动,此时的加速度与向上减速的加速度相等:aA4=aA3=2g,加速度的方向向下,
向下运动到达MN的时间:${t}_{4}={t}_{3}=\sqrt{\frac{h}{2g}}$
向下的位移:${x}_{A4}={x}_{A3}=\frac{1}{2}h$,此时第二次进入电场.
B球和杆向下的速度:${v}_{B4}={v}_{B3}+{a}_{B}{t}_{4}=3\sqrt{2gh}$
向下的位移:${x}_{B4}=\frac{({v}_{B3}+{v}_{B4})}{2}•{t}_{4}$
联立得:${x}_{B4}=\frac{17}{6}h$
从A球第一次进入电场到A球第二次进入电场,A、B两球的运动曲线如图3,该过程的总时间: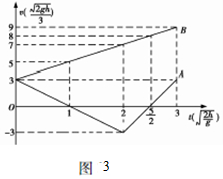
t=t1+t2+t3+t4
杆的长度:l=(xB1-xA1)+(xB2-xA2)+(xB3-xA3)+(xB4-xA4)
联立得:t=$3\sqrt{\frac{2h}{g}}$,l=12h
答:(1)A球运动过程中的最大电势能是3mgh;
(2)从A球第一次进入电场到A球第二次进入电场的过程中经历的时间是$3\sqrt{\frac{2h}{g}}$,杆的长度是12h.
点评 本题有一定的难度,要注意受力的变化导致加速度变化,运动过程要分析清楚,分阶段计算,比较好.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案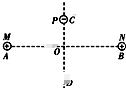 如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N分别固定在A、B两点,O为A、B连线的中点,C、D在AB的垂直平分线上.在C点处由静止释放一个带负电的小球P(不改变原来的电场分布),此后P在C点和D点之间来回运动,则( )
如图所示,在光滑绝缘水平面上,两个带等量正电的点电荷M、N分别固定在A、B两点,O为A、B连线的中点,C、D在AB的垂直平分线上.在C点处由静止释放一个带负电的小球P(不改变原来的电场分布),此后P在C点和D点之间来回运动,则( )| A. | 若小球P在经过C点时带电量突然减小则它将会运动到CD两点之外 | |
| B. | 若小球P在经过C、O之间某处时带电量减小,则它将会运动到CD两点之外 | |
| C. | 若小球P在经过C点时,点电荷M、N的带电量同时等量增大,则它将会运动到CD两点之外 | |
| D. | 若小球P在经过C、O之间某处时,点电荷M、N的带电量同时等量增大,则它以后不可能再运动到C点 |
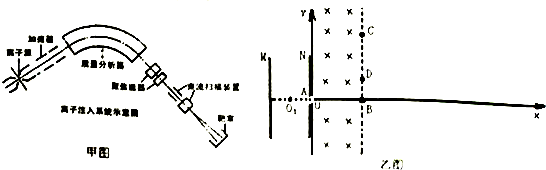
 如图1所示,光滑平行竖直金属导轨AB、CD相距L,在A、C之间接一个阻值为R的电阻,在两导轨间abcd矩形区域内有垂直导轨平面竖直向上、磁感应强度大小为B、宽为5d的匀强磁场.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合),现用一个竖直向上的力F拉导体棒,使它由静止开始运动,已知导体棒离开磁场前已开始做匀速直线运动,导体棒与导轨始终垂直且保持良好接触,导轨电阻不计,F随导体棒与初始位置的距离x变化的情况如图2所示,重力加速度为g,下列判断正确的是( )
如图1所示,光滑平行竖直金属导轨AB、CD相距L,在A、C之间接一个阻值为R的电阻,在两导轨间abcd矩形区域内有垂直导轨平面竖直向上、磁感应强度大小为B、宽为5d的匀强磁场.一质量为m、电阻为r、长度也为L的导体棒放在磁场下边界ab上(与ab边重合),现用一个竖直向上的力F拉导体棒,使它由静止开始运动,已知导体棒离开磁场前已开始做匀速直线运动,导体棒与导轨始终垂直且保持良好接触,导轨电阻不计,F随导体棒与初始位置的距离x变化的情况如图2所示,重力加速度为g,下列判断正确的是( )| A. | 导体棒离开磁场时速度大小为$\frac{2mg(R+r)}{{B}^{2}{L}^{2}}$ | |
| B. | 导体棒经过磁场的过程中,通过电阻R的电荷量为$\frac{5BLd}{R}$ | |
| C. | 离开磁场时导体棒两端电压为$\frac{2mgR}{BL}$ | |
| D. | 导体棒经过磁场的过程中,电阻R产生焦耳热为$\frac{9mgdR{B}^{4}{L}^{4}-2{m}^{3}{g}^{2}R(R+r)^{2}}{{B}^{4}{L}^{4}(R+r)}$ |
 如图所示,斜面体固定在水平面上,斜面粗糙.一带正电的绝缘物体自斜面上端由静止释放,设物体由顶端滑到底端所用的时间为t.下列几种情况能使物体下滑时间t减少的是(设整个运动过程中物体始终没有离开斜面)( )
如图所示,斜面体固定在水平面上,斜面粗糙.一带正电的绝缘物体自斜面上端由静止释放,设物体由顶端滑到底端所用的时间为t.下列几种情况能使物体下滑时间t减少的是(设整个运动过程中物体始终没有离开斜面)( )| A. | 在物体运动所在的空间加上竖起向下的匀强电场 | |
| B. | 在物体运动所在的空间加上水平向右的匀强电场 | |
| C. | 在物体运动所在的空间加上垂直纸面向里的匀强磁场 | |
| D. | 在物体运动所在的空间加上垂直纸面向外的匀强磁场 |
 如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )
如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )| A. | 剪断绳子的瞬间,物体A的加速度为2g | |
| B. | 弹簧恢复原长时,物体A的速度最大 | |
| C. | 弹簧压缩到最短时,物体A的加速度为零 | |
| D. | 剪断绳子后,物体A速度为零时,地面对B的力最大 |
| A. | 微粒在下落过程中动能逐渐增加,重力势能逐渐减小 | |
| B. | 微粒落入电场中,电势能逐渐增大,其增加量为$\frac{1}{2}$qU | |
| C. | 微粒下落过程中,重力做功为mg(h+$\frac{d}{2}$),电场力做功为-$\frac{1}{2}$qU | |
| D. | 微粒的重力势能全部转化为电势能 |
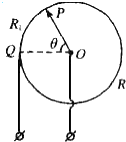 将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.
将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.