题目内容
20.如图(a)所示,水平放置的平行金属板AB间的距离d=0.1m,板长L=0.3m,在金属板的左端竖直放置一带有小孔的挡板,小孔恰好位于AB板的正中间,距金属板右端x=0.5m处竖直放置一足够大的荧光屏,现在AB板间加如图(b)所示的方波形电压,已知U0=1.0×102V,在挡板的左侧,有大量带正电的相同粒子以平行于金属板方向的速度持续射向挡板,粒子的质量m=1.0×10-7kg,电荷量q=1.0×10-2C,速度大小均为v0=1.0×104m/s,带电粒子的重力不计,则:
(1)求粒子从进入电场到打中荧光屏所经历的时间;
(2)求在t=0时刻进入的粒子飞出电场时垂直于极板方向的位移大小,及速度与水平方向夹角的正切值;
(3)若撤去挡板,求由正极板边缘、且从t=1×10-5s时刻进入电场的粒子打到荧光屏上的位置距O点的距离.
分析 (1)根据匀速直线运动位移时间关系求解时间;
(2)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出电子的运动时间,求出粒子在电场中的偏移量;应用运动的合成与分解,牛顿第二定律与运动学公式可以求出粒子的速度方向;
(3)求出粒子在电场中的偏移量以及出电场时竖直方向的速度大小,然后求出粒子打到荧光屏上的位置距O点的距离.
解答 解:(1)粒子水平方向速度不变,作匀速直线运动,
粒子从进入电场到打中荧光屏所经历的时间为:t0=$\frac{L+x}{{v}_{0}}=\frac{0.3+0.5}{1.0×1{0}^{4}}s$=8×10-5s;
(2)粒子在电场中运动的时间为:$t′=\frac{L}{{v}_{0}}=\frac{0.3}{1.0×1{0}^{4}}s=3×1{0}^{-5}s$,
0时刻进入的粒子竖直方向上先作匀加速直线运动,用时t1=2×10-5s;再作匀减速直线运动,用时t2=1×10-5s,
加速度大小相等,为:a=$\frac{q{U}_{0}}{md}=\frac{1.0×1{0}^{-2}×1.0×1{0}^{2}}{1.0×1{0}^{-7}×0.1}m/{s}^{2}$=1×108m/s2,
侧移量:d1=$\frac{1}{2}a{t}_{1}^{2}+a{t}_{1}{t}_{2}-\frac{1}{2}a{t}_{2}^{2}$=3.5×10-2m,
射出时竖直方向的速度大小为${v}_{y}=a{t}_{1}-a{t}_{2}=1{0}^{8}(2×1{0}^{-5}-1×1{0}^{-5})$=1×103m/s,
正切值tanθ=$\frac{{v}_{y}}{{v}_{0}}=\frac{1}{10}$;
(3)粒子从t=1×10-5s时刻进入电场,在第一个1×10-5s向负极板加速运动、在第二个1×10-5s向负极板减速运动,在第三个1×10-5s向负极板加速运动;
所以出电场时的偏离正极板的位移:y1'=$\frac{1}{2}a{t}^{2}×3$=0.005×3=0.015m
出电场时沿竖直方向的速度为$v{′}_{1}=at=1{0}^{3}s$,
场外沿竖直方向的位移:y2'=$v{′}_{1}t′=1{0}^{3}×\frac{0.5}{1{0}^{4}}m$=0.05m
结果y'=0.065m-0.05m=0.015m.
答:(1)粒子从进入电场到打中荧光屏所经历的时间为8×10-5s;
(2)在t=0时刻进入的粒子飞出电场时垂直于极板方向的位移大小为3.5×10-2m,速度与水平方向夹角的正切值为$\frac{1}{10}$;
(3)若撤去挡板,求由正极板边缘、且从t=1×10-5s时刻进入电场的粒子打到荧光屏上的位置距O点的距离为0.015m.
点评 解决在偏转场中问题,通常由类平抛运动规律求解,要能熟练运用运动的合成与分解的方法研究,分析时要充分运用匀加速运动位移的比例关系和运动的对称性,来求解竖直分位移.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )
如题图所示,物体A、B的质量相等,物体B刚好与地面接触.现剪断绳子OA,下列说法正确的是( )| A. | 剪断绳子的瞬间,物体A的加速度为2g | |
| B. | 弹簧恢复原长时,物体A的速度最大 | |
| C. | 弹簧压缩到最短时,物体A的加速度为零 | |
| D. | 剪断绳子后,物体A速度为零时,地面对B的力最大 |
 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )| A. | 编号为①的粒子在磁场区域内运动的时间为$\frac{πm}{qB}$ | |
| B. | 编号为②的粒子在磁场区域内运动的时间为$\frac{πm}{qB}$ | |
| C. | 三个粒子进入磁场的速度依次增加 | |
| D. | 三个粒子在磁场内运动的时间依次增加 |
 图中虚线PQ上方有一磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外.O是PQ上一点,在纸面内从O点向磁场区域的任意方向连续发射速率为v0的粒子,粒子电荷量为q、重力为m.现有两个粒子先后射入磁场中并恰好在M点相遇,MO与PQ间夹角为60°,不计粒子重力及粒子间的相互作用,则下列说法正确的是( )
图中虚线PQ上方有一磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向外.O是PQ上一点,在纸面内从O点向磁场区域的任意方向连续发射速率为v0的粒子,粒子电荷量为q、重力为m.现有两个粒子先后射入磁场中并恰好在M点相遇,MO与PQ间夹角为60°,不计粒子重力及粒子间的相互作用,则下列说法正确的是( )| A. | 两个粒子从O点射入磁场的时间间隔可能为$\frac{2πm}{3qB}$ | |
| B. | 两个粒子射入磁场的方向分别与PQ成30°和60°角 | |
| C. | 在磁场中运动的粒子离边界的最大距离为$\frac{2m{v}_{0}}{qB}$ | |
| D. | 垂直PQ射入磁场中的粒子在磁场中的运动时间最长 |

| A. | 物块在4 s内位移是8 m | B. | 物块的质量是1 kg | ||
| C. | 物块与水平面间动摩擦因数是0.4 | D. | 物块在4 s内电势能减少了14 J |
| A. | 220V | B. | 220$\sqrt{2}$V | C. | 110V | D. | 110$\sqrt{2}$V |
 如图,A、B为半径R=1m的四分之一光滑绝缘竖直圆弧轨道,在四分之一圆弧区域内存在着E=1×106 V/m、竖直向上的匀强电场,有一质量m=1kg、带电荷量q=+1.4×10-5C的物体(可视为质点),从A点的正上方距离A点H处由静止开始自由下落(不计空气阻力),BC段为长L=2m、与物体间动摩擦因数μ=0.2的粗糙绝缘水平面.(取g=10m/s2)
如图,A、B为半径R=1m的四分之一光滑绝缘竖直圆弧轨道,在四分之一圆弧区域内存在着E=1×106 V/m、竖直向上的匀强电场,有一质量m=1kg、带电荷量q=+1.4×10-5C的物体(可视为质点),从A点的正上方距离A点H处由静止开始自由下落(不计空气阻力),BC段为长L=2m、与物体间动摩擦因数μ=0.2的粗糙绝缘水平面.(取g=10m/s2) 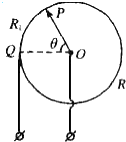 将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$.
将阻值为16Ω的均匀电阻丝变成一闭合圆环,在圆环上取Q为固定点,P为滑键,构成一圆形滑动变阻器,如图所示.要使Q、P间的电阻先后为4Ω和3Ω,则对应的θ角应分别是π和$\frac{π}{2}$或$\frac{3}{2}π$. 如图所示,在xOy直角坐标系中,在x=-L和y轴之间有垂直于纸面向里的匀强磁场,在x=2L和y轴之间有沿x轴负方向的匀强电场,电场强度大小为E,在x轴上S(-L,0)有一质量为m,电荷量为q的带正电的粒子,粒子的速率大小为v0,沿x轴正方向射出后经磁场和电场偏转后到达x=2L上时,速度刚好沿y轴正向,不计粒子的重力,求磁场的磁感应强度.
如图所示,在xOy直角坐标系中,在x=-L和y轴之间有垂直于纸面向里的匀强磁场,在x=2L和y轴之间有沿x轴负方向的匀强电场,电场强度大小为E,在x轴上S(-L,0)有一质量为m,电荷量为q的带正电的粒子,粒子的速率大小为v0,沿x轴正方向射出后经磁场和电场偏转后到达x=2L上时,速度刚好沿y轴正向,不计粒子的重力,求磁场的磁感应强度.