题目内容
2.三个同学根据不同的实验条件,进行了“探究平抛运动规律”的实验:
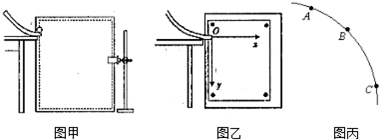
(1)甲同学采用如图(1)所示的装置.用小锤打击弹性金属片,金属片把A球沿水平方向弹出,同时B球被松开,自由下落,观察到两球同时落地,改变小锤打击的力度,即改变A球被弹出时的速度,两球仍然同时落地,这说明平抛运动在竖直方向做自由落体运动.
(2)乙同学采用如图(2)所示的装置.两个相同的弧形轨道M、N,分别用于发射小铁球 P、Q,其中N的末端与可看作光滑的水平板相切;两轨道上端分别装有电磁铁C、D;调节电磁铁C、D的高度,使AC=BD,从而保证小铁球P、Q在轨道出口处的水平初速度v0相等,现将小铁球P、Q分别吸在电磁铁C、D上,然后切断电源,使两小铁球能以相同的初速度v0同时分别从轨道M、N的下端射出.实验可观察到的现象应是P球落地时刚好和Q球相遇;仅仅改变弧形轨道M的高度,重复上述实验,仍能观察到相同的现象,这说明平抛运动在水平方向做匀速直线运动.
(3)丙同学采用频闪摄影的方法拍摄到如图(3)所示的“小球做平抛运动”的照片.图中每个小方格的边长为10cm,则由图可求得拍摄时每0.1s曝光一次,该小球运动到图中位置2时速度大小为2.5m/s(g取10m/s2).
分析 (1)同时让A球做平抛运动,B球做自由落体运动.若两小球同时落地,则说明平抛运动竖直方向是自由落体运动.
(2)同时让P球做平抛运动,Q球做匀速运动,若两小球相碰,则说明平抛运动水平方向是匀速运动.
(3)平抛运动可以分解为水平方向的匀速直线运动与竖直方向的自由落体运动,在竖直方向上应用匀变速运动的推论可以求出频闪照相的时间间隔,由匀速运动的速度公式可以求出小球的初速度;由匀变速运动的推论可以求出瞬时速度,然后求出小球的速度.
解答 解:(1)在打击金属片时,金属片把A球沿水平方向弹出,做平抛运动,同时B球被松开,做自由落体运动,两小球同时落地,说明A球与B球在竖直方向的运动规律相同,即:说明平抛运动竖直方向是自由落体运动.
(2)两小铁球P、Q能以相同的初速度同时分别从轨道下端水平射出,小球P做平抛运动,小球Q在水平方向做匀速直线运动,可以看到:P球落地时刚好和Q球相遇;当同时改变两小球滚下的高度时,仍能相碰,这说明:初速度相同时,平抛运动在水平方向的运动规律与匀速运动规律相同,即:说明平抛运动在水平方向做匀速直线运动.
(3)平抛运动可看成竖直方向自由落体运动与水平方向匀速直线运动;
在竖直方向:由△h=gt2可得:
t=$\sqrt{\frac{0.1}{10}}=0.1s$
水平方向:由x=v0t得:
v0=$\frac{2×0.1}{0.1}=2m/s$
2位置竖直方向速度为:${v}_{y}=\frac{{h}_{13}}{2t}=\frac{0.3}{0.2}=1.5m/s$
所以打点2的速度为:${v}_{2}=\sqrt{{{v}_{0}}^{2}{{+v}_{y}}^{2}}=\sqrt{{2}^{2}+1.{5}^{2}}=2.5m/s$
故答案为:(1)平抛运动在竖直方向做自由落体运动;
(2)P球落地时刚好和Q球相遇;平抛运动在水平方向做匀速直线运动;
(3)0.1,2.5.
点评 该实验设计的巧妙,有创新性,使复杂问题变得更直观,因此在平抛运动的规律探究活动中不一定局限于课本实验的原理,要重视学生对实验的创新.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | 相撞后某些速度增大的碎片,要靠近地球运动 | |
| B. | 相撞后某些速度增大的碎片,要远离地球运动 | |
| C. | 相撞后所有的碎片都要靠近地球运动 | |
| D. | 相撞后所有的碎片都要远离地球运动 |
 振动电机实际上是一个偏心轮,简化模型如图1所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力的大小为N,小球在最高点的速度大小为v,N-v2图象如图2所示.下列说法正确的是( )
振动电机实际上是一个偏心轮,简化模型如图1所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力的大小为N,小球在最高点的速度大小为v,N-v2图象如图2所示.下列说法正确的是( )| A. | 小球的质量为$\frac{a}{b}$R | |
| B. | 当v=$\sqrt{b}$时,球对杆有向下的压力 | |
| C. | 当v<$\sqrt{b}$时,球对杆有向上的拉力 | |
| D. | 若c=2b,则此时杆对小球的弹力大小为2a |
 某双星系统由两颗恒星构成,质量分别为m1和m2,距中心的距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )
某双星系统由两颗恒星构成,质量分别为m1和m2,距中心的距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )| A. | 它们运转的周期相同 | B. | 它们的线速度大小相同 | ||
| C. | m2>m1 | D. | 它们的加速度大小相同 |
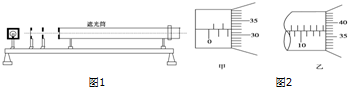
(1)若用20分度的游标卡尺测得遮光片的宽度b,如图乙所示,则b=9.50mm.
(2)若用d表示A点到导轨底端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,在误差范围内,若公式$\frac{{b}^{2}}{{t}^{2}}=\frac{2gsh}{d}$成立,就可以验证机械能守恒定律(用题中给出的物理量符号表示).
(3)多次改变光电门的位置,每次均令滑块自A点静止释放下滑,测量相应的s与t值,结果如下表所示:
| 1 | 2 | 3 | 4 | 5 | |
| s(m) | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| t(ms) | 8.22 | 7.12 | 6.00 | 5.81 | 5.38 |
| $\frac{1}{{t}^{2}}$(102s-2) | 1.48 | 1.97 | 2.78 | 2.96 | 3.45 |