题目内容
8. 某同学在“用单摆测重力加速度”的实验中进行了如下的操作:
某同学在“用单摆测重力加速度”的实验中进行了如下的操作:(1)关于安装仪器及测量时的一些实验操作,下列说法中正确的是C.
A.用米尺测出摆线的长度,记为摆长l
B.先将摆球和摆线放在水平桌面上测量摆长l,再将单摆悬挂在铁架台上
C.使摆线偏离竖直方向某一角度α(接近5°),然后静止释放摆球
D.测出摆球两次通过最低点的时间间隔记为此单摆振动的周期
(2)测量多组周期T、摆长L数值后,画出T2-L图象如图乙,此图线斜的物理意义是C.
A.g B.$\frac{1}{g}$ C.$\frac{4{π}^{2}}{g}$ D.$\frac{g}{4{π}^{2}}$
(3)与重力加速度的真实值比较,发现测量结果偏小,分析原因可能是BC.
A.振幅偏小
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.将摆线长当成了摆长
D.实验中误将29次全振动数记为30次.
分析 (1)单摆的摆长等于摆线的长度与摆球半径之和;单摆应固定在铁架台上;摆线偏角不超过5°;应测量30次或50次全振动的时间,再求出每次全振动的时间,作为周期,可减小测量误差.
(2)根据单摆的周期公式得出T2-L的关系式,结合关系式得出图线斜率的含义.
(3)根据单摆的周期公式得出重力加速度的表达式,通过测量误差确定重力加速度的误差.
解答 解:(1)A.用米尺测出摆线的长度,用游标卡尺测量摆球的直径,摆线的长度加上摆球的半径记为摆长l,故A错误.
B.先将摆球和摆线连接好,固定在铁架台上,否则摆长变化,测量的误差较大,故B错误.
C.使摆线偏离竖直方向某一角度α(接近5°),从静止释放摆球让摆球振动,故C正确.
D、测出摆球两次通过最低点的时间间隔记为此单摆振动的周期,误差较大,为了减小误差,应采用累积法,即测量30次或50次全振动的时间,再求出每次全振动的时间,作为周期.故D错误.
故选:C.
(2)根据$T=2π\sqrt{\frac{L}{g}}$得,${T}^{2}=\frac{4{π}^{2}L}{g}$,可知图线的斜率为$\frac{4{π}^{2}}{g}$,故选:C.
(3)根据$T=2π\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$,
A、振幅偏小,不影响重力加速度的测量,故A错误.
B、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,则摆长的测量值偏小,导致重力加速度的测量值偏小,故B正确.
C、将摆线长当成了摆长,则摆长的测量值偏小,导致重力加速度的测量值偏小,故C正确.
D、实验中误将29次全振动数记为30次,周期的测量值偏小,导致重力加速度的测量值偏大,故D错误.
故选:BC.
故答案为:(1)C,(2)C,(3)BC.
点评 解决本题的关键知道实验的原理以及注意事项,对于图线问题,一般的解题思路是得出物理量的关系式,从而分析判断.

 发散思维新课堂系列答案
发散思维新课堂系列答案 如图所示,在天花板与墙壁之间用长为L的轻绳通过光滑轻质挂钩悬挂着一重力为G的物体,已知悬点A、B与墙角C之间的距离相等,且L=2AC,则关于轻绳上弹力的大小和方向,下列说法正确的是( )
如图所示,在天花板与墙壁之间用长为L的轻绳通过光滑轻质挂钩悬挂着一重力为G的物体,已知悬点A、B与墙角C之间的距离相等,且L=2AC,则关于轻绳上弹力的大小和方向,下列说法正确的是( )| A. | 大小为aG,与竖直方向之间的夹角为60° | |
| B. | 大小为$\frac{\sqrt{3}}{3}$G,与竖直方向之间的夹角为30° | |
| C. | 大小为$\frac{2\sqrt{3}}{3}$G,与竖直方向之间的夹角为45° | |
| D. | 大小为$\frac{\sqrt{3}}{3}$G,与竖立方向之间的夹角为30° |
 如图所示,斜劈劈尖顶着竖直墙壁静止与水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )
如图所示,斜劈劈尖顶着竖直墙壁静止与水平面上,现将一小球从图示位置静止释放,不计一切摩擦,则在小球从释放到落至地面的过程中,下列说法正确的是( )| A. | 斜劈对小球的弹力做负功 | |
| B. | 斜劈与小球组成的系统机械能不守恒 | |
| C. | 小球的机械能增加 | |
| D. | 斜劈的机械能增加 |
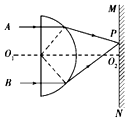 如图所示,O1O2是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于O1O2轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于O1O2放置的光屏,沿O1O2方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )
如图所示,O1O2是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于O1O2轴等距且平行的两束不同单色细光束,从玻璃体右方射出后的光路如图所示,MN是垂直于O1O2放置的光屏,沿O1O2方向不断左右移动光屏,可在屏上得到一个光斑P,根据该光路图,下列说法正确的是( )| A. | 该玻璃体对A光的折射率比对B光的折射率小 | |
| B. | A光从空气进入该玻璃体后,其频率变高 | |
| C. | 在该玻璃体中,A光比B光的传播速度大 | |
| D. | 在真空中,A光的波长比B光的波长长 |

| A. | 卫星a运行周期大于24 h | |
| B. | 卫星a运行周期小于24 h | |
| C. | 在地面附近发射卫星b的速度为11.2 km/s | |
| D. | 卫星a的运行速度可能为7.9 km/s |
| A. | 在下落过程中,同一时刻甲的速度比乙的速度大 | |
| B. | 在下落过程中,同一时刻甲的速度比乙的速度小 | |
| C. | 甲、乙在空气中运动的时间之比为1:2 | |
| D. | 甲落地时,乙距地面的高度为H |
 如图为一个摆长为1.00m的单摆在地面的共振曲线.取π=3.14,则当地的重力加速度g=9.86m/s2(保留三位有效数字).如果保持单摆不变,将该单摆从地面移到高山顶,共振曲线振幅最大值的横坐标向左移(填“向左移”、“不变”或“向右移”)
如图为一个摆长为1.00m的单摆在地面的共振曲线.取π=3.14,则当地的重力加速度g=9.86m/s2(保留三位有效数字).如果保持单摆不变,将该单摆从地面移到高山顶,共振曲线振幅最大值的横坐标向左移(填“向左移”、“不变”或“向右移”)
 从受力特点来看,做简谐运动的物体所受到的回复力F=-kx,负号表示回复力F的方向始终与物体偏离平衡位置的位移x的方向相反,k为比例系数.相关文献表明,力学中的-切做简谐运动的物体,其往复运动的周期均可利用公式T=2π$\sqrt{\frac{m}{k}}$求解,m是做简谐运动的物体质量,k为回复力公式中的比例系数.
从受力特点来看,做简谐运动的物体所受到的回复力F=-kx,负号表示回复力F的方向始终与物体偏离平衡位置的位移x的方向相反,k为比例系数.相关文献表明,力学中的-切做简谐运动的物体,其往复运动的周期均可利用公式T=2π$\sqrt{\frac{m}{k}}$求解,m是做简谐运动的物体质量,k为回复力公式中的比例系数.