题目内容
12. 如图所示,密闭容器有进气口和出气口可以和外部连通,容器的容积为V0,将进气口和出气口关闭,此时内部封闭气体的压强为P0,将气体缓慢加热,使气体温度由T0=300K升至T1=350K.
如图所示,密闭容器有进气口和出气口可以和外部连通,容器的容积为V0,将进气口和出气口关闭,此时内部封闭气体的压强为P0,将气体缓慢加热,使气体温度由T0=300K升至T1=350K.①求此时气体的压强:
②保持T1=350K不变,缓慢由出气口抽出部分气体,使气体压强再变回到P0.求容器内剩余气体的质量与原来总质量的比值.
分析 ①封闭气体发生了等容变化,故根据查理定律列式可求出气体压强;
②抽气过程可等效为等温膨胀过程,根据玻意耳定律可求出总体积,从而求出剩余气体的质量与原来总质量的比值.
解答 解:①设升温后气体的压强为p1,
气体加热前:内部封闭气体的压强为p0,气体温度为T0=300K
气体加热前:气体温度为T1=350K
加热过程,体积不变,由查理定律得:$\frac{{P}_{0}}{{T}_{0}}=\frac{{P}_{1}}{{T}_{1}}$
代入数据得:p1=$\frac{7}{6}$p0 ①
②抽气过程可等效为等温膨胀过程,设膨胀后气体的总体积为V,由玻意耳定律得:p1V0=p0V ②
①②联立得:V=$\frac{7}{6}$V0…①
设剩余气体的质量与原来总质量的比值为k,由题意得:k=$\frac{{V}_{0}}{V}$…③
②③联立得:k=$\frac{6}{7}$
答:①求此时气体的压强为$\frac{7}{6}$p0②容器内剩余气体的质量与原来总质量的比值为$\frac{6}{7}$.
点评 解答这类问题时正确选择状态,弄清变化类型,正确分析状态参量的变化,然后列方程求解.

练习册系列答案
相关题目
3.在测电源电动势和内阻的实验中,用电源、电阻箱、电压表连成如图1所示的电路,一位同学记录的6组数据如表:

请在图2方格纸上选择适当的坐标轴画出图线,并根据图线读出电源的电动势E=1.5V,求得电源的内阻r=0.35Ω
| R/Ω | 2.0 | 3.0 | 6.0 | 10 | 15 | 20 |
| U/V | 1.30 | 1.36 | 1.41 | 1.48 | 1.49 | 1.50 |

请在图2方格纸上选择适当的坐标轴画出图线,并根据图线读出电源的电动势E=1.5V,求得电源的内阻r=0.35Ω
20. 如图所示,质量为m,电量为q的小球在电场强度E的匀强电场中,以初速度υ0沿直线ON做匀变速运动,直线ON与水平面的夹角为30°.若小球在初始位置的电势能为零,重力加速度为g,且mg=Eq,则下面说法中正确的是( )
如图所示,质量为m,电量为q的小球在电场强度E的匀强电场中,以初速度υ0沿直线ON做匀变速运动,直线ON与水平面的夹角为30°.若小球在初始位置的电势能为零,重力加速度为g,且mg=Eq,则下面说法中正确的是( )
 如图所示,质量为m,电量为q的小球在电场强度E的匀强电场中,以初速度υ0沿直线ON做匀变速运动,直线ON与水平面的夹角为30°.若小球在初始位置的电势能为零,重力加速度为g,且mg=Eq,则下面说法中正确的是( )
如图所示,质量为m,电量为q的小球在电场强度E的匀强电场中,以初速度υ0沿直线ON做匀变速运动,直线ON与水平面的夹角为30°.若小球在初始位置的电势能为零,重力加速度为g,且mg=Eq,则下面说法中正确的是( )| A. | 电场方向竖直向上 | B. | 小球运动的加速度大小为g | ||
| C. | 小球运动的最大高度为$\frac{{{V}_{0}}^{2}}{2g}$ | D. | 小球电势能的最大值为$\frac{m{{V}_{0}}^{2}}{2}$ |
7. 如图甲所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为FN,小球在最高点的速度大小为v,FN-v2图象如乙图所示.下列说法正确的是( )
如图甲所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为FN,小球在最高点的速度大小为v,FN-v2图象如乙图所示.下列说法正确的是( )
 如图甲所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为FN,小球在最高点的速度大小为v,FN-v2图象如乙图所示.下列说法正确的是( )
如图甲所示,一轻杆一端固定在O点,另一端固定一小球,在竖直平面内做半径为R的圆周运动.小球运动到最高点时,杆与小球间弹力大小为FN,小球在最高点的速度大小为v,FN-v2图象如乙图所示.下列说法正确的是( )| A. | 当地的重力加速度大小为$\frac{R}{b}$ | B. | 小球的质量为$\frac{a}{b}$R | ||
| C. | v2=c时,杆对小球弹力方向向上 | D. | 若c=2b.则杆对小球弹力大小为a |
17. 如图所示,水平放置的细杆上套一细环A,环A和带电球B间用一绝缘轻质细绳相连,质量分别为mA、mB,B球受到水平电场力的作用,细绳与竖直方向的夹角为θ,A环与B球都保持静止,则下列说法正确的是( )
如图所示,水平放置的细杆上套一细环A,环A和带电球B间用一绝缘轻质细绳相连,质量分别为mA、mB,B球受到水平电场力的作用,细绳与竖直方向的夹角为θ,A环与B球都保持静止,则下列说法正确的是( )
 如图所示,水平放置的细杆上套一细环A,环A和带电球B间用一绝缘轻质细绳相连,质量分别为mA、mB,B球受到水平电场力的作用,细绳与竖直方向的夹角为θ,A环与B球都保持静止,则下列说法正确的是( )
如图所示,水平放置的细杆上套一细环A,环A和带电球B间用一绝缘轻质细绳相连,质量分别为mA、mB,B球受到水平电场力的作用,细绳与竖直方向的夹角为θ,A环与B球都保持静止,则下列说法正确的是( )| A. | B球受到的电场力大小为mBgsinθ | |
| B. | 当场强增大时,轻质绳对B球的拉力仍保持不变 | |
| C. | 当场强增大时,杆对A环的摩擦力保持不变 | |
| D. | 当场强增大时,杆对A环的支持力保持不变 |
4. 如图所示的电路中,C为一平行板电容器,闭合开关S,给电容器充电,当电路中电流稳定之后,下列说法正确的是( )
如图所示的电路中,C为一平行板电容器,闭合开关S,给电容器充电,当电路中电流稳定之后,下列说法正确的是( )
 如图所示的电路中,C为一平行板电容器,闭合开关S,给电容器充电,当电路中电流稳定之后,下列说法正确的是( )
如图所示的电路中,C为一平行板电容器,闭合开关S,给电容器充电,当电路中电流稳定之后,下列说法正确的是( )| A. | 保持开关S闭合,把滑动变阻器R1的滑片向上滑动,电流表的示数变大,电压表的示数变小 | |
| B. | 保持开关S闭合,不论滑动变阻器R1的滑片是否滑动,都有电流流过R2 | |
| C. | 保持开关S闭合,将电容器上下极板距离稍微拉大的过程中,R2中有电流从a流向b | |
| D. | 断开开关S,若此时刚好有一带电油滴P静止在两平行板电容器之间,将电容器上下极板的距离稍微拉大的过程中,油滴将向上运动 |
1. 如图所示为甲、乙两个物体运动的v-t图象,若两物体从同一地点出发,且最终运动的位移相等,甲的初速度是乙的初速度的两倍,则下列说法正确的是( )
如图所示为甲、乙两个物体运动的v-t图象,若两物体从同一地点出发,且最终运动的位移相等,甲的初速度是乙的初速度的两倍,则下列说法正确的是( )
 如图所示为甲、乙两个物体运动的v-t图象,若两物体从同一地点出发,且最终运动的位移相等,甲的初速度是乙的初速度的两倍,则下列说法正确的是( )
如图所示为甲、乙两个物体运动的v-t图象,若两物体从同一地点出发,且最终运动的位移相等,甲的初速度是乙的初速度的两倍,则下列说法正确的是( )| A. | 甲、乙都沿负方向运动 | |
| B. | 甲、乙在运动过程中一定会相遇 | |
| C. | 甲、乙在t0时刻相距最远 | |
| D. | 乙运动的时间一定是甲运动的时间的2倍 |
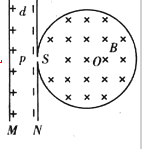 一圆筒的横截面如图所示,其圆心为O,筒内有垂直于纸面向里的匀强磁场,磁感应强度为B.圆筒左侧有相距为d的平行金属板M、N其中M板带正电荷,N板带等量负电荷.质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放,经N板的小孔S以速度v沿半径SO方向射入磁场中.粒子与圈筒发生2次碰撞后仍从S孔射出.设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的情况下,求:
一圆筒的横截面如图所示,其圆心为O,筒内有垂直于纸面向里的匀强磁场,磁感应强度为B.圆筒左侧有相距为d的平行金属板M、N其中M板带正电荷,N板带等量负电荷.质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放,经N板的小孔S以速度v沿半径SO方向射入磁场中.粒子与圈筒发生2次碰撞后仍从S孔射出.设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的情况下,求: 图示为公交车在沿直线向前运动时的一个场景,此时乘客身体向前倾斜,此时的汽车正处于减速(选填“加速”或“减速”)阶段.
图示为公交车在沿直线向前运动时的一个场景,此时乘客身体向前倾斜,此时的汽车正处于减速(选填“加速”或“减速”)阶段.