��Ŀ����
2��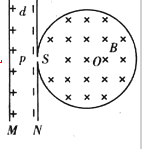 һԲͲ�ĺ������ͼ��ʾ����Բ��ΪO��Ͳ���д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��ԲͲ��������Ϊd��ƽ�н�����M��N����M�������ɣ�N�����������ɣ�����Ϊm�������Ϊq�Ĵ�����������M���Ե��P���ɾ�ֹ�ͷţ���N���С��S���ٶ�v�ذ뾶SO��������ų��У�������ȦͲ����2����ײ���Դ�S���������������ԲͲ��ײ������û�ж�����ʧ���ҵ�������ֲ��䣬�ڲ�������������£���
һԲͲ�ĺ������ͼ��ʾ����Բ��ΪO��Ͳ���д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��ԲͲ��������Ϊd��ƽ�н�����M��N����M�������ɣ�N�����������ɣ�����Ϊm�������Ϊq�Ĵ�����������M���Ե��P���ɾ�ֹ�ͷţ���N���С��S���ٶ�v�ذ뾶SO��������ų��У�������ȦͲ����2����ײ���Դ�S���������������ԲͲ��ײ������û�ж�����ʧ���ҵ�������ֲ��䣬�ڲ�������������£�����1��M��N��糡ǿ��E�Ĵ�С��
��2��ԲͲ�İ뾶R��
��3��������M��N���糡ǿ��E�Ĵ�С�������Դ�M���Ե��P���ɾ�ֹ�ͷţ�ʹ�����Խ���ԲͲ������S������糡�ڼ���ԲͲ��ײ5�Σ���������P�����������P����ʱ��t��
���� ��1����������ǿ�糡���ڼ����˶����糡�������������Ӷ��ܵ����ӣ����ݶ��ܶ�����ʽU=Ed��ⳡǿE�Ĵ�С��
��2�������ڴų��������������ṩ����������ʽ����������˶��Ĺ켣�뾶���ٸ������⣬��ȷ���������˶��Ĺ켣�����ݼ��ι�ϵд�����ӵİ뾶��ų��İ뾶�Ĺ�ϵ���Ӷ����ԲͲ�İ뾶R��
��3������S������糡�ڼ���ԲͲ��ײ5�Σ����ݼ��ι�ϵ��֪��5��ײ���S��ԲͲ6�ȷ֣�����뾶��������������ų�ʱ���ٶȣ������ڴų����˶���ʱ��Ϊһ�����ڣ������˶�ѧ������ʽ����ڵ糡���˶���ʱ�伴����⣮
��� �⣺��1���������ĵ�ѹΪU���ɶ��ܶ����ã�qU=$\frac{1}{2}$mv2-0����
����ǿ�糡�е��Ʋ���糡ǿ�ȵĹ�ϵ�ã�U=Ed����
������ʽ�ɵã�E=$\frac{m{v}^{2}}{2qd}$����
��2�����ӽ���ų����ִ�S����������ݼ��ι�ϵ��֪������ײ���S��ԲͲ���ȷ֣�
�������ڴų����˶��Ĺ���뾶Ϊr�������������ṩ���������ã�
$Bqv=m\frac{{v}^{2}}{r}$
���ݼ��ι�ϵr=$\sqrt{3}R$
������ʽ����ã�R=$\frac{\sqrt{3}mv}{3qB}$
��3������S������糡�ڼ���ԲͲ��ײ5�Σ����ݼ��ι�ϵ��֪��5��ײ���S��ԲͲ6�ȷ֣�����Բ���˶��İ뾶r��=R��
����$Bqv��=m\frac{{v��}^{2}}{r��}$
��ã�$v��=\frac{BqR}{m}$
�����ڴų����˶���ʱ��Ϊһ������t${\;}_{1}=T=\frac{2��m}{Bq}$��
�����ڵ糡�м��ٵ�ʱ��${t}_{2}=\frac{d}{\frac{v��}{2}}=\frac{2dm}{BqR}$��
����������P�����������P����ʱ��t=${t}_{1}+2{t}_{2}=\frac{2��m}{Bq}+\frac{4dm}{BqR}$=$\frac{2��m}{Bq}+\frac{4\sqrt{3}d}{v}$��
�𣺣�1��M��N��糡ǿ��E�Ĵ�СΪ$\frac{m{v}^{2}}{2qd}$��
��2��ԲͲ�İ뾶RΪ$\frac{\sqrt{3}mv}{3qB}$��
��3��������P�����������P����ʱ��tΪ$\frac{2��m}{Bq}+\frac{4\sqrt{3}d}{v}$��
���� �������Ĺؼ��Ǹ�����Ŀ��Ҫ����ȷ���������˶��Ĺ켣�������ݼ��ι�ϵд�����ӵİ뾶��ų��İ뾶�Ĺ�ϵ������Կռ�˼ά������Ҫ��Ƚϸߣ�

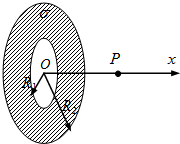 ��ͼ��һ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ�����ܲ������˴��ij�ǿE�����������ͨ��һ�������������������б���ʽ�ĺ����������жϣ���������жϣ�E�ĺ�������ʽӦΪ��������
��ͼ��һ���ڡ���뾶�ֱ�ΪR1��R2��Բ��״���ȴ���ƽ�棬�䵥λ���������Ϊ�ң�ȡ��������OΪԭ�㣬�Դ�ֱ�ڻ��������Ϊx�ᣮ�����������P��O��ľ���Ϊx��P��糡ǿ�ȵĴ�СΪE���������E���ĸ�����ʽ��ʽ��kΪ������������������ֻ��һ���Ǻ����ģ�����ܲ������˴��ij�ǿE�����������ͨ��һ�������������������б���ʽ�ĺ����������жϣ���������жϣ�E�ĺ�������ʽӦΪ��������| A�� | E=2��k�ң�$\frac{{R}_{1}}{\sqrt{{x}^{2}+{{R}_{1}}^{2}}}$-$\frac{{R}_{2}}{\sqrt{{x}^{2}+{{R}_{2}}^{2}}}$��x | B�� | E=2��k�ң�$\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$�\$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x | ||
| C�� | E=2��k�ң�$\frac{{R}_{1}}{\sqrt{{x}^{2}+{{{R}_{1}}^{2}}^{\;}}}$+$\frac{{R}_{2}}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$�� | D�� | E=2��k�ң�$\frac{1}{\sqrt{{x}^{2}+{R}_{1}^{2}}}$+$\frac{1}{\sqrt{{x}^{2}+{R}_{2}^{2}}}$��x |

| A�� | ��a��������������� | B�� | ��b��������������� | ||
| C�� | ��c�������ױ�̥ | D�� | ��d�������ױ�̥ |
 ��һλͬѧ�����ð�����ͷ��ر��ⶨ��Դ�綯�ƺ��ڵ����ʵ���У����ʵ���������������ͼ��������ֽ�ϻ���ͼ�ߣ��������Դ�綯��E=3.0V���ڵ���r=0.5����
��һλͬѧ�����ð�����ͷ��ر��ⶨ��Դ�綯�ƺ��ڵ����ʵ���У����ʵ���������������ͼ��������ֽ�ϻ���ͼ�ߣ��������Դ�綯��E=3.0V���ڵ���r=0.5����| ������� | 1 | 2 | 3 | 4 | 5 |
| I��A�� | 0.40 | 0.80 | 1.00 | 1.60 | 2.00 |
| U��V�� | 2.80 | 2.60 | 2.50 | 2.20 | 2.00 |
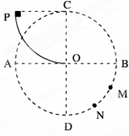 ����ֱƽ������һ�뾶ΪR��Բ������AB��CD�ֱ�Ϊˮƽ����ֱ������ֱ����BM��MN��ND���λ�����ȣ���һ�ķ�֮һԲ����ֱԲ��������뾶Ҳ��R��Բ����C�㣬����¶���O����AB���У�
����ֱƽ������һ�뾶ΪR��Բ������AB��CD�ֱ�Ϊˮƽ����ֱ������ֱ����BM��MN��ND���λ�����ȣ���һ�ķ�֮һԲ����ֱԲ��������뾶Ҳ��R��Բ����C�㣬����¶���O����AB���У�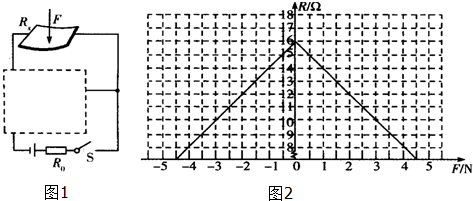
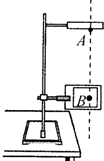 ijͬѧ��Ƴ���ͼ��ʾ��ʵ��װ������֤��е���غ㶨�ɣ�ͨ����������Ƶ�С�����A���������䣬��������о��������Bʱ��ͨ����֮�����ĺ����ʱ����ͼ��δ��������¼����ʱ��t���ú��̶ȳ߲��AB֮��ľ���h�����α꿨�߲��С�����ֱ��d���������ٶ�Ϊg��ʵ��ǰӦ���������λ��ʹС�����������������ͨ��������еļ�������С����ͨ�������ʱ��˳ʱ�ٶ�v=$\frac{d}{t}$�������е���غ㶨�ɳ�������d��t��h��g���ڹ�ϵʽΪ$\frac{d^2}{{2{t^2}}}=gh$��
ijͬѧ��Ƴ���ͼ��ʾ��ʵ��װ������֤��е���غ㶨�ɣ�ͨ����������Ƶ�С�����A���������䣬��������о��������Bʱ��ͨ����֮�����ĺ����ʱ����ͼ��δ��������¼����ʱ��t���ú��̶ȳ߲��AB֮��ľ���h�����α꿨�߲��С�����ֱ��d���������ٶ�Ϊg��ʵ��ǰӦ���������λ��ʹС�����������������ͨ��������еļ�������С����ͨ�������ʱ��˳ʱ�ٶ�v=$\frac{d}{t}$�������е���غ㶨�ɳ�������d��t��h��g���ڹ�ϵʽΪ$\frac{d^2}{{2{t^2}}}=gh$�� ��ͼ��ʾ���ܱ������н����ںͳ����ڿ��Ժ��ⲿ��ͨ���������ݻ�ΪV0���������ںͳ����ڹرգ���ʱ�ڲ���������ѹǿΪP0�������建�����ȣ�ʹ�����¶���T0=300K����T1=350K��
��ͼ��ʾ���ܱ������н����ںͳ����ڿ��Ժ��ⲿ��ͨ���������ݻ�ΪV0���������ںͳ����ڹرգ���ʱ�ڲ���������ѹǿΪP0�������建�����ȣ�ʹ�����¶���T0=300K����T1=350K��