题目内容
16.如图甲所示,n=10匝的圆形线圈,线圈两端与同一平面内放置的光滑平行导轨两端相连,导轨宽L=0.5m,长也为L的导体棒MN垂直放在导轨上且与导轨良好接触.电路中接入的电阻R=0.5Ω,导轨、导体棒与线圈电阻均不计.在导轨平面范围内有匀强磁场B1=0.8T垂直穿过,方向垂直纸面向外.在线圈内有垂直纸面向内的匀强磁场B2,线圈中的磁通量随时间变化的图象如图乙所示.请根据下列条件分别求解: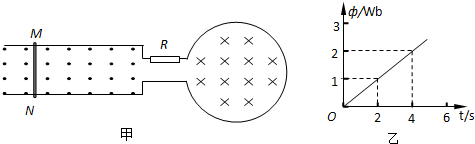
(1)如导体棒MN在外力作用下保持静止,求t=2s时刻导体棒受到的安培力.
(2)如导体棒MN在外界作用下,在匀强磁场B1中沿导轨方向作匀速直线运动,运动速度大小为v=25m/s,求t=2s时刻导体棒受到的安培力.
分析 (1)根据法拉第电磁感应定律求得感应电动势,结合闭合电路欧姆定律,求得电路的中电流,再根据安培力表达式F=BIL,即可求解;
(2)根据法拉第电磁感应定律,求得切割感应电动势,与感应电动势,结合楞次定律,从而确定总电动势是两者之差,还是之和,再由闭合电路欧姆定律,与安培力表达式,即可求解.
解答 解:(1)据图得:$\frac{△Φ}{△t}$=$\frac{2}{4}$=0.5Wb/s
由法拉第电磁感应定律,线圈产生感应电动势E1=n$\frac{△Φ}{△t}$=10×0.5 V=5V;
再根据闭合电路欧姆定律,则有感应电流大小为 I=$\frac{E}{R}$=$\frac{5}{0.5}$A=10A;
t=2s时刻导体棒受到的安培力的大小 F=B1IL=0.8×10×0.5=4N;
(2)在匀速磁场中向右作匀速直线运动,产生动生电动势为 E2=B1Lv=0.8×0.5×25=10V;
根据楞次定律可知,动生电动势与感生电动势方向相同,则电路中总感应电动势E=E1+E2=15V;
回路中感应电流的大小为 I′=$\frac{E}{R}$=30A
那么t=2s时刻,导体棒受到的安培力的大小 F′=B1I′L=0.8×30×0.5=12N;
答:
(1)导体棒MN在外力作用下保持静止,则t=2s时刻导体棒受到的安培力的大小为4N,
(2)t=2s时刻导体棒受到的安培力的大小为12N.
点评 考查法拉第电磁感应定律与闭合电路欧姆定律的应用,掌握安培力表达式的内容,注意动生电动势与感生电动势的区别,及总感应电动势的求法是解题的关键.

练习册系列答案
相关题目
6. 如图,质量m=1kg、可看成质点的小物块静止在水平桌面上,其与桌子边缘相距0.4m,物块与桌面间的动摩擦因数为μ=0.4.现用F=5N的水平力向右推小物块,为了使它从桌子上掉下,取g=10m/s2,则力F的作用时间至少为( )
如图,质量m=1kg、可看成质点的小物块静止在水平桌面上,其与桌子边缘相距0.4m,物块与桌面间的动摩擦因数为μ=0.4.现用F=5N的水平力向右推小物块,为了使它从桌子上掉下,取g=10m/s2,则力F的作用时间至少为( )
 如图,质量m=1kg、可看成质点的小物块静止在水平桌面上,其与桌子边缘相距0.4m,物块与桌面间的动摩擦因数为μ=0.4.现用F=5N的水平力向右推小物块,为了使它从桌子上掉下,取g=10m/s2,则力F的作用时间至少为( )
如图,质量m=1kg、可看成质点的小物块静止在水平桌面上,其与桌子边缘相距0.4m,物块与桌面间的动摩擦因数为μ=0.4.现用F=5N的水平力向右推小物块,为了使它从桌子上掉下,取g=10m/s2,则力F的作用时间至少为( )| A. | 0.8s | B. | 1.0s | C. | $\frac{2}{5}$$\sqrt{5}$s | D. | $\frac{2}{5}$$\sqrt{10}$s |
7. 如图所示虚线a,b,c代表电场中三个等势面,相邻等势面之间的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P,Q是这条轨迹上的两点,据此可知( )
如图所示虚线a,b,c代表电场中三个等势面,相邻等势面之间的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P,Q是这条轨迹上的两点,据此可知( )
 如图所示虚线a,b,c代表电场中三个等势面,相邻等势面之间的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P,Q是这条轨迹上的两点,据此可知( )
如图所示虚线a,b,c代表电场中三个等势面,相邻等势面之间的电势差相等,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P,Q是这条轨迹上的两点,据此可知( )| A. | 三个等势面中,Q的电势较高 | B. | 带电质点通过P点时电势能较大 | ||
| C. | 带电质点通过P点时动能较大 | D. | 带电质点通过P点时加速度较大 |
4.按频率由小到大,电磁波谱的排列顺序是( )
| A. | 红外线、无线电波、紫外线、可见光、γ射线、X射线 | |
| B. | 无线电波、红外线、可见光、X射线、γ射线 | |
| C. | γ射线、X射线、紫外线、可见光、红外线、无线电波 | |
| D. | 无线电波、紫外线、可见光、红外线、X射线、γ射线 |
11.对于做匀速圆周运动的质点,下列说法正确的是( )
| A. | 根据公式a=$\frac{{V}^{2}}{r}$,可知其向心加速度a与半径r成反比 | |
| B. | 根据公式a=rω2,可知其向心加速度a与半径r成正比 | |
| C. | 根据公式ω=$\frac{V}{r}$,可知其角速度ω与半径r成反比 | |
| D. | 根据公式ω=2πn,可知其角速度ω与转数n成正比 |
 如图所示,水平面上固定一个倾角为θ的斜面,已知sinθ=$\frac{\sqrt{5}}{5}$,一个小球从斜面上某一位置P处斜向上抛出,到达斜面顶端Q处时速度恰好变为水平方向,已知P、Q间的距离为L=2$\sqrt{5}$m,重力加速度为g=10m/s2,求:
如图所示,水平面上固定一个倾角为θ的斜面,已知sinθ=$\frac{\sqrt{5}}{5}$,一个小球从斜面上某一位置P处斜向上抛出,到达斜面顶端Q处时速度恰好变为水平方向,已知P、Q间的距离为L=2$\sqrt{5}$m,重力加速度为g=10m/s2,求: 如图所示,AB和CDO都是处于竖直平面内的光滑圆弧形轨道,OA处于水平位置,AB是半径为R=2m的$\frac{1}{4}$圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性档板.D为CDO轨道的中点.BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H处自由落下.(取g=10m/s2)
如图所示,AB和CDO都是处于竖直平面内的光滑圆弧形轨道,OA处于水平位置,AB是半径为R=2m的$\frac{1}{4}$圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性档板.D为CDO轨道的中点.BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H处自由落下.(取g=10m/s2) 正弦交变电流图象如图所示,其感应电动势的最大值为50V,周期为0.08s.当线圈转速变为原来的$\sqrt{2}$倍时,所产生交变电动势的有效值为50V.周期为$\frac{\sqrt{2}}{25}$s.
正弦交变电流图象如图所示,其感应电动势的最大值为50V,周期为0.08s.当线圈转速变为原来的$\sqrt{2}$倍时,所产生交变电动势的有效值为50V.周期为$\frac{\sqrt{2}}{25}$s. 如图甲所示,矩形线框abcd固定放在匀强磁场中,磁场方向与线圈平面垂直,磁感应强度B随时间t变化的图象如图乙所示.设t=0时刻,磁感应强度的方向垂直纸面向里,图中I表示线圈中感应电流的大小,F表示线框ab边所受的安培力的大小(规定电流沿顺时针方向为正,ab边中所受的安培力方向向左为正),则可能正确的是( )
如图甲所示,矩形线框abcd固定放在匀强磁场中,磁场方向与线圈平面垂直,磁感应强度B随时间t变化的图象如图乙所示.设t=0时刻,磁感应强度的方向垂直纸面向里,图中I表示线圈中感应电流的大小,F表示线框ab边所受的安培力的大小(规定电流沿顺时针方向为正,ab边中所受的安培力方向向左为正),则可能正确的是( )


