题目内容
8.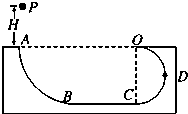 如图所示,AB和CDO都是处于竖直平面内的光滑圆弧形轨道,OA处于水平位置,AB是半径为R=2m的$\frac{1}{4}$圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性档板.D为CDO轨道的中点.BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H处自由落下.(取g=10m/s2)
如图所示,AB和CDO都是处于竖直平面内的光滑圆弧形轨道,OA处于水平位置,AB是半径为R=2m的$\frac{1}{4}$圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性档板.D为CDO轨道的中点.BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H处自由落下.(取g=10m/s2)(1)当H=1.4m时,问此球第一次到达D点对轨道的压力大小.
(2)当H=1.4m时,试通过计算判断此球是否会脱离CDO轨道.如果会脱离轨道,求脱离前球在水平轨道经过的路程.如果不会脱离轨道,求静止前球在水平轨道经过的路程.
(3)为使小球仅仅与弹性板碰撞二次,且小球不会脱离CDO轨道,问H的取值范围.
分析 (1)先对从P到D过程根据动能定理列式求解D点速度,然后由支持力提供向心力列式求解支持力.
(2)先判断能够第一次到达O点,第二次来到D点是沿着原路返回,然后判断能否第三次到达D点,最后对全程根据动能定理列式求解总路程.
(3)先判断出小球能够发生第二次碰撞的条件,然后判断出小球仅仅能发生第二次碰撞,而满足不会离开CDO轨道的条件,综合即可.
解答 解:(1)设小球第一次到达D的速度VD,P到D点的过程对小球根据动能定理列式,有:
mg(H+r)-μmgL=$\frac{1}{2}$mVD2
在D点对小球列牛顿第二定律:FN=m$\frac{{v}_{D}^{2}}{r}$
联立解得:FN=32N
(2)第一次来到O点,速度V1,P到O点的过程对小球根据动能定理列式,有:
mgH-μmgL=$\frac{1}{2}$mV12
解得:V12=12
要能通过O点,须mg<m$\frac{{v}^{2}}{r}$
临界速度VO2=10
故第一次来到O点之前没有脱离,第二次来到D点是沿着原路返回,设第三次来到D点的动能EK
对之前的过程根据动能定理列式,有:
mg(H+r)-3μmgL=EK
代入解得:EK=0
故小球一直没有脱离CDO轨道
设此球静止前在水平轨道经过的路程S
对全过程根据动能定理列式,有:
mg(H+R)-μmgS=0
解得:S=8.5m
(3)为使小球与挡板碰撞第二次,需满足:$mgH-3μmgL≥\frac{1}{2}m{v}_{0}^{2}$
代入数据解得:H≥2.9m
为使小球与仅仅挡板碰撞二次,且小球不会脱离CDO轨道,需满足:
mg(H+r)-5μmgL≤0
代入数据解得:H≤3m
故:2.9m≤H≤3.0m
答:(1)当H=1.4m时,此球第一次到达D点对轨道的压力大小为32N.
(2)当H=1.4m时,此球不会脱离CDO轨道,静止前球在水平轨道经过的路程为8.5m.
(3)为使小球仅仅与弹性板碰撞二次,且小球不会脱离CDO轨道,H需满足:2.9m≤H≤3.0m
点评 本题关键是结合动能定理和向心力公式判断物体的运动情况,注意临界点D和Q位置的判断.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | 同一物体运动时比静止时惯性大 | |
| B. | 物体惯性大小与物体运动与否无关 | |
| C. | 同样大小的力作用在不同的物体上,速度变化慢的物体惯性大 | |
| D. | 在月球上把物体举起要比在地球上容易,说明同一物体在月球上惯性比在地球上小 |
| A. | 总与初速度方向一致 | B. | 总与推力方向一致 | ||
| C. | 总与合外力的方向一致 | D. | 总与末速度方向一致 |
| A. | 30J | B. | 100J | C. | 70J | D. | 130J |
 半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.
半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g.