��Ŀ����
20����������¹�����ԭ���ڲ����ӵ��˶������ģ���˹����о���̽��ԭ�ӽṹ��һ����Ҫ;�������������ŵ�ܿ��Ի����ԭ�ӹ��ף����ݲ������ۿ��Ժܺõؽ�����ԭ�ӹ��IJ�����������֪��ԭ�ӵĻ�̬����ΪE1������̬����ΪEn=$\frac{E_1}{n^2}$������n=2��3��4����1885�꣬�Ͷ�ĩ�Ե�ʱ��֪���ڿɼ������������������˷�����������Щ���ߵIJ����ܹ���һ����ʽ��ʾ�������ʽд��$\frac{1}{��}=R��\frac{1}{2^2}-\frac{1}{n^2}��$��n=3��4��5������ʽ��R������²������������ʽ��Ϊ�Ͷ�ĩ��ʽ����h��ʾ���ʿ˳�����c��ʾ����еĹ��٣�����²�����R���Ա�ʾΪ��������| A�� | -$\frac{E_1}{2hc}$ | B�� | $\frac{E_1}{2hc}$ | C�� | -$\frac{E_1}{hc}$ | D�� | $\frac{E_1}{hc}$ |
���� �Ӹ��ܼ�����ܼ�ԾǨ��������ӣ�����Ĺ��������������ܼ�����ܼ�����$\frac{1}{��}=R��\frac{1}{2^2}-\frac{1}{n^2}��$��n=3��4��5���������²�������
��� �⣺��n��m����n��mԾǨ���ͷŹ��ӣ���$\frac{{E}_{1}}{{n}^{2}}-\frac{{E}_{1}}{{m}^{2}}=hv$��
��Ϊ$v=\frac{c}{��}$����${E}_{1}��\frac{1}{{n}^{2}}-\frac{1}{{m}^{2}}��=h\frac{c}{��}$��
��$h\frac{c}{��}$=hcR��$\frac{1}{{2}^{2}}-\frac{1}{{n}^{2}}$������-E1=hcR��
�����²�����R=$-\frac{{E}_{1}}{hc}$��
��ѡ��C��
���� �������Ĺؼ�֪����������յĹ��������������ܼ�����ܼ��֪������Ƶ���벨���Ĺ�ϵ������������ã��ѶȲ���

��ϰ��ϵ�д�
�����Ŀ
3�� ��ͼ��ʾ�ռ�����һ�㹻����ˮƽ��Ե��MN���ڰ�����Ϸ��д�ֱ��ֽ������ĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų�������һ������Ϊm��������Ϊq�Ĵ�������������ٶ�v�Ӱ��ϵ�E����ֱ���Ͻ���ų�������ÿ�δ��Ϻ��ٶȷ�����ԭ�����෴���ٶȴ�С��Ϊԭ����һ�룬�������ӵĵ������䣬���ӳ�����ڶ����뵲����ײ������ʱ��;������ľ���ֱ�Ϊ�����������ܵ�����������������
��ͼ��ʾ�ռ�����һ�㹻����ˮƽ��Ե��MN���ڰ�����Ϸ��д�ֱ��ֽ������ĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų�������һ������Ϊm��������Ϊq�Ĵ�������������ٶ�v�Ӱ��ϵ�E����ֱ���Ͻ���ų�������ÿ�δ��Ϻ��ٶȷ�����ԭ�����෴���ٶȴ�С��Ϊԭ����һ�룬�������ӵĵ������䣬���ӳ�����ڶ����뵲����ײ������ʱ��;������ľ���ֱ�Ϊ�����������ܵ�����������������
 ��ͼ��ʾ�ռ�����һ�㹻����ˮƽ��Ե��MN���ڰ�����Ϸ��д�ֱ��ֽ������ĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų�������һ������Ϊm��������Ϊq�Ĵ�������������ٶ�v�Ӱ��ϵ�E����ֱ���Ͻ���ų�������ÿ�δ��Ϻ��ٶȷ�����ԭ�����෴���ٶȴ�С��Ϊԭ����һ�룬�������ӵĵ������䣬���ӳ�����ڶ����뵲����ײ������ʱ��;������ľ���ֱ�Ϊ�����������ܵ�����������������
��ͼ��ʾ�ռ�����һ�㹻����ˮƽ��Ե��MN���ڰ�����Ϸ��д�ֱ��ֽ������ĴŸ�Ӧǿ�ȴ�СΪB����ǿ�ų�������һ������Ϊm��������Ϊq�Ĵ�������������ٶ�v�Ӱ��ϵ�E����ֱ���Ͻ���ų�������ÿ�δ��Ϻ��ٶȷ�����ԭ�����෴���ٶȴ�С��Ϊԭ����һ�룬�������ӵĵ������䣬���ӳ�����ڶ����뵲����ײ������ʱ��;������ľ���ֱ�Ϊ�����������ܵ�����������������| A�� | $\frac{2��m}{qB}$��$\frac{4mv}{qB}$ | B�� | $\frac{2��m}{qB}$��$\frac{3mv}{qB}$ | C�� | $\frac{3��m}{2qB}$��$\frac{4mv}{qB}$ | D�� | $\frac{3��m}{2qB}$��$\frac{3mv}{qB}$ |
11�����ڿ�ѧ���������������������Ź㷺��Ӧ�ã����з���ʵ��Ӧ�õ��ǣ�������
| A�� | �ڹ��ά���ڴ���ͼ�������ù��ɫɢ���� | |
| B�� | �����ı�ƽ���������ѧƽ���ƽ���̶������ù���������� | |
| C�� | ��ѧ��ͷ�ϵ���Ĥ�����ù�ĸ������� | |
| D�� | ���ֹ���ᷢ��ƫ������ |
5�������ijһ�ߴ�ƽ�ף�����ٶ�Ϊv0������ٶ�ΪV�������������������ڿ��з���ʱ��Ϊ��������
| A�� | $\frac{{{v_0}-v}}{2g}$ | B�� | $\frac{{v-{v_0}}}{2g}$ | C�� | $\frac{{\sqrt{{v^2}-v_0^2}}}{2g}$ | D�� | $\frac{{\sqrt{{v^2}-v_0^2}}}{g}$ |
9�������������˶������У���е���غ���ǣ�������
| A�� | �شֲ�б�������»� | B�� | �شֲ�б�������ϻ� | ||
| C�� | �شֲ�б������»� | D�� | �ع⻬б�������»� |
 ��ͼ��ʾ���ڰ뾶ΪR�İ�Բ�����ڵĹ⻬�����ϣ�һ����Ϊm��С���Խ��ٶȦ���ˮƽ����������Բ���˶�����С�����ڹ��ƽ�������ĸ߶�h�����������ٶ�Ϊg��
��ͼ��ʾ���ڰ뾶ΪR�İ�Բ�����ڵĹ⻬�����ϣ�һ����Ϊm��С���Խ��ٶȦ���ˮƽ����������Բ���˶�����С�����ڹ��ƽ�������ĸ߶�h�����������ٶ�Ϊg�� ��ͼ��ʾ��ˮƽ�����Ϲ̶�һ��Ե�⻬������abcd-a��b��c��d�䣬��abΪ15m����adΪ10m����aa��Ϊ5m��MN��PQ��ad�ƽ�У���aN��NQ��Qb����붼Ϊ5m��һ���뾶ΪR=5m��$\frac{1}{4}$Բ���Ĺ⻬��Ե�������ֱ�̶���Բ���������ߵ�E������Բ��O��ͬһˮƽ���ϣ�MΪ��װ����cd���е㣬����MNQP��PQbc������ֱ�������ǿ�ų����Ÿ�Ӧǿ�ȴ�С�ֱ�ΪB1=1T��B2=2T�������෴���߽�MN��PQ���ų�����E�㾲ֹ�ͷ�һ����m1=0.1kg���������q=0.1C��С��g=10m/s2����
��ͼ��ʾ��ˮƽ�����Ϲ̶�һ��Ե�⻬������abcd-a��b��c��d�䣬��abΪ15m����adΪ10m����aa��Ϊ5m��MN��PQ��ad�ƽ�У���aN��NQ��Qb����붼Ϊ5m��һ���뾶ΪR=5m��$\frac{1}{4}$Բ���Ĺ⻬��Ե�������ֱ�̶���Բ���������ߵ�E������Բ��O��ͬһˮƽ���ϣ�MΪ��װ����cd���е㣬����MNQP��PQbc������ֱ�������ǿ�ų����Ÿ�Ӧǿ�ȴ�С�ֱ�ΪB1=1T��B2=2T�������෴���߽�MN��PQ���ų�����E�㾲ֹ�ͷ�һ����m1=0.1kg���������q=0.1C��С��g=10m/s2����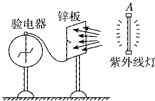 ��ͼ��ʾ��һ�������п����������A����һ�����ߵ�����п�壬�صƺ�ָ�뱣��һ��ƫ�ǣ���ʱп������磮���������������ʹ�����ָ��ص��㣬������ͬǿ�ȵ��ƵƷ����Ļƹ�����п�壬�����ָ����ƫת����ô��������ǿ�ȸ���ĺ����ߵ�����п�壬�ɹ۲쵽�����ָ���ޣ���С����ޡ���ƫת��
��ͼ��ʾ��һ�������п����������A����һ�����ߵ�����п�壬�صƺ�ָ�뱣��һ��ƫ�ǣ���ʱп������磮���������������ʹ�����ָ��ص��㣬������ͬǿ�ȵ��ƵƷ����Ļƹ�����п�壬�����ָ����ƫת����ô��������ǿ�ȸ���ĺ����ߵ�����п�壬�ɹ۲쵽�����ָ���ޣ���С����ޡ���ƫת�� ��ͼ��ʾ��������Ȧ����ǿ�ų�����OO�����ͼʾλ�ÿ�ʼ����ת������֪��ͼʾλ��ת��$\frac{��}{6}$ʱ����Ȧ�и�Ӧ�綯�ƴ�СΪ10V����
��ͼ��ʾ��������Ȧ����ǿ�ų�����OO�����ͼʾλ�ÿ�ʼ����ת������֪��ͼʾλ��ת��$\frac{��}{6}$ʱ����Ȧ�и�Ӧ�綯�ƴ�СΪ10V����