题目内容
15. 如图所示,水平地面上固定一绝缘光滑长方体abcd-a′b′c′d′,长ab为15m,宽ad为10m,高aa′为5m,MN、PQ与ad相互平行,且aN、NQ、Qb间距离都为5m.一个半径为R=5m的$\frac{1}{4}$圆弧的光滑绝缘轨道被竖直固定,圆弧轨道的最高点E与它的圆心O在同一水平线上,M为该装置与cd的切点,区域MNQP、PQbc存在竖直方向的匀强磁场,磁感应强度大小分别为B1=1T和B2=2T,方向相反,边界MN、PQ处无磁场.从E点静止释放一质量m1=0.1kg,带正电荷q=0.1C的小球.g=10m/s2.求:
如图所示,水平地面上固定一绝缘光滑长方体abcd-a′b′c′d′,长ab为15m,宽ad为10m,高aa′为5m,MN、PQ与ad相互平行,且aN、NQ、Qb间距离都为5m.一个半径为R=5m的$\frac{1}{4}$圆弧的光滑绝缘轨道被竖直固定,圆弧轨道的最高点E与它的圆心O在同一水平线上,M为该装置与cd的切点,区域MNQP、PQbc存在竖直方向的匀强磁场,磁感应强度大小分别为B1=1T和B2=2T,方向相反,边界MN、PQ处无磁场.从E点静止释放一质量m1=0.1kg,带正电荷q=0.1C的小球.g=10m/s2.求:(1)小球刚到达M点时,对圆弧管道的压力大小;
(2)小球从E点静止释放后由M点运动到落地的时间t;(π≈3)
(3)若在b′处有一静止的小滑块,其质量为m2=0.01kg,与地面间的动摩擦因数?=0.9.当小球刚过M时,对小滑块施加一水平恒力F,作用一段时间后撤去该恒力,使之在小球刚落地时两者$\underset{恰}{•}$$\underset{好}{•}$相遇,此时小滑块的速度也刚好减小到零.求恒力F的大小?($\sqrt{3}$≈1.7,$\sqrt{2.5}$≈$\sqrt{2.6}$≈1.6)
分析 (1)小球从E到M的过程,机械能守恒,根据机械能守恒定律求出小球到M点时的速度,结合牛顿第二定律与向心力表达式,及牛顿第三定律,即可求解;
(2)根据小球做匀速圆周运动,结合半径公式,及平抛运动规律,并由几何关系,即可求解.
(3)滑块先做匀加速运动,后做匀减速运动,作出v-t图象,求出最大速度,再由速度关系求解F的大小.
解答 解:(1)小球从释放到M点的过程,由机械能守恒有:
m1gR=$\frac{1}{2}{m}_{1}{v}^{2}$
代入数据解得:v=10m/s
在M点,由牛顿第二定律有:
F-m1g=m1$\frac{{v}^{2}}{R}$
解得:F=3N 根据牛顿第三定律,小球到达M点时对管道的压力为3N.
根据牛顿第三定律,小球到达M点时对管道的压力为3N.
(2)①小球的运动情况如图所示,
设其在B1中的运动半径为R1,运动时间为t1.有:B1qv=m1$\frac{{v}^{2}}{{R}_{1}}$
代入数据解得:R1=10m
由图可知,小球在B1中做圆运动的圆心角为30°
所以 t1=$\frac{\frac{π}{6}{R}_{1}}{v}$=$\frac{π}{6}$≈0.5s
②设小球在B2中的运动半径为R2,运动时间为t2.有:B2qv=m2$\frac{{v}^{2}}{{R}_{2}}$
解代入数据得:R2=5m
小球在B2中做圆运动的圆心角为60°
所以t2=$\frac{\frac{π}{3}{R}_{2}}{v}$=$\frac{π}{6}$≈0.5s
③小球离开B2区域后做平抛运动,设小球做平抛运动的时间为t3.则有:hbb′=$\frac{1}{2}g{t}_{3}^{2}$
解得:t3=1s
所以,小球从M点到落地的时间为:t=t1+t2+t3≈2s
(3)①小球做平抛运动的水平位移为:x1=vt3=10m
根据题意,小滑块的运动是先匀加速再匀减速,其位置关系如图所示.
由图可知小滑块的总位移 x=$\sqrt{{x}_{1}^{2}+{x}_{2}^{2}-2{x}_{1}{x}_{2}cos120°}$
其中 x2=R1cos30°=5$\sqrt{3}$m
解得 x=$\sqrt{175+50\sqrt{3}}$m≈$\sqrt{260}$m≈16m
②小滑块的v-t图象形状如右下图所示,设小滑
块加速阶段的时间为t0,最大速度为vm,则
由位移关系有 x=$\frac{1}{2}{v}_{m}t$
速度关系有 vm=$\frac{F-μ{m}_{2}g}{{m}_{2}}$t0=$\frac{μ{m}_{2}g}{{m}_{2}}$(t-t0)
解得vm=16m/s,t0=$\frac{2}{9}$s,作用力F=0.81N.
答:(1)小球刚到达M点时,对圆弧管道的压力大小是3N.
(2)小球从M点到落地的时间t是2s.
(3)恒力F的大小为0.81N.
点评 本题是复杂磁场与力学综合题,要按时间顺序正确分析小球的运动情况,对于磁场,关键定圆心,找半径,对于相遇问题,关键要找两个物体之间的关系.


| A. | A质点做匀加速直线运动 | |
| B. | A、B两质点在8s末相遇 | |
| C. | B质点前4s做减速运动,4秒后做加速运动 | |
| D. | B质点先沿负方向做直线运动,后沿正方向做直线运动 |
| A. | -$\frac{E_1}{2hc}$ | B. | $\frac{E_1}{2hc}$ | C. | -$\frac{E_1}{hc}$ | D. | $\frac{E_1}{hc}$ |
| A. | 一定质量的理想气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加 | |
| B. | 液体表面张力产生的原因是液体表面层分子较稀疏,分子间的距离大于r0,分子间的作用表现为引力 | |
| C. | 干湿泡湿度计的干泡显示的温度低于湿泡显示的温度,这是湿泡外纱布中的水蒸发吸热的结果 | |
| D. | 空气的相对湿度定义为水的饱和蒸汽压与相同温度时空气中所含水蒸气的压强之比 |
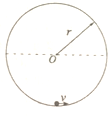 如图所示,宇航员在地球表面完成以下实验:在固定的竖直光滑圆弧轨道内部的最低点,给质量为m的小球水平初速度v,小球恰能在竖直平面内做完整的圆周运动,而宇航员在某星球表面重复上述实验时发现小球只能上升至圆心等高处.已知该星球半径为地球半径的2倍,小球可视为质点,可求得该星球和地球的密度之比为( )
如图所示,宇航员在地球表面完成以下实验:在固定的竖直光滑圆弧轨道内部的最低点,给质量为m的小球水平初速度v,小球恰能在竖直平面内做完整的圆周运动,而宇航员在某星球表面重复上述实验时发现小球只能上升至圆心等高处.已知该星球半径为地球半径的2倍,小球可视为质点,可求得该星球和地球的密度之比为( )| A. | 5:4 | B. | 4:5 | C. | 5:1 | D. | 1:5 |
| A. | 220 V指的是交流电压的峰值 | |
| B. | 变压器可以变换交流电的电压、功率和频率 | |
| C. | 发电机转子的转速为3 000 r/min | |
| D. | 采用远距离高压输电可减小输电线的电阻及电线上的电流 |
 如图所示,竖直平面内的轨道是由倾角为θ的粗糙直轨道AB和半径为R的光滑圆弧轨道BCD相切于B点而构成的,E为轨道的最低点.质量为m的小物块(可视为质点)从直轨道上的P点由静止释放,物块沿轨道向下运动.物块与轨道AB间的动摩擦因数为μ.
如图所示,竖直平面内的轨道是由倾角为θ的粗糙直轨道AB和半径为R的光滑圆弧轨道BCD相切于B点而构成的,E为轨道的最低点.质量为m的小物块(可视为质点)从直轨道上的P点由静止释放,物块沿轨道向下运动.物块与轨道AB间的动摩擦因数为μ. 图中的竖直圆筒固定不动,粗筒横截面积是细筒的4倍,细筒足够长.粗筒中A、B两轻质活塞间封有空气,气柱长l=20cm.活塞A上方的水银深H=10cm,两活塞与筒壁间的摩擦不计.大气压强p0=75cmHg.用外力F竖直向上托住活塞B,使之处于静止状态.水银面与粗筒上端相平.现缓慢升高温度,直至水银的一半进入细筒中,求:
图中的竖直圆筒固定不动,粗筒横截面积是细筒的4倍,细筒足够长.粗筒中A、B两轻质活塞间封有空气,气柱长l=20cm.活塞A上方的水银深H=10cm,两活塞与筒壁间的摩擦不计.大气压强p0=75cmHg.用外力F竖直向上托住活塞B,使之处于静止状态.水银面与粗筒上端相平.现缓慢升高温度,直至水银的一半进入细筒中,求:


