题目内容
13.随着科学的发展,人们生活中走过的桥正在不断的变化,图甲是古代的石拱桥,图乙是现代的斜拉桥.无论哪种桥与物理知识都有密切联系,请根据所学知识回答下列两个问题.
(1)若石拱桥简化为图丙所示的模型,正中央有一质量为m的对称楔形石块,侧面与竖直方向的夹角均为θ,重力加速度为g,若接触面间的摩擦力忽略不计,则石块侧面所受弹力的大小为多少?
(2)斜拉桥的塔柱两侧有许多钢索,它们的一端都系在塔柱上.对于每组对称钢索,它们的上端可以看成系在一起,即两根钢索对塔柱的拉力F1、F2作用在同一点.它们合起来对塔柱的作用效果应该让塔柱好像受到一个竖直向下的力F一样,如果斜拉桥塔柱两侧的钢索不能呈对称分布,且钢索AC和AB与竖直方向的夹角分别为α和β,如图丁所示,则要保持塔柱所受的合力竖直向下,钢索AC、AB的拉力FAC与FAB之比应为多少?
分析 (1)对石块受力分析,根据共点力平衡条件,运用合成法列式求解;
(2)将钢索AC、AB的拉力FAC、FAB进行合成,合力竖直向下,根据平行四边形定则作图后根据几何关系列式求解.
解答  解:(1)楔形石块受力如图戊所示,根据力的合成可得:mg=2Fcos(90°-θ)
解:(1)楔形石块受力如图戊所示,根据力的合成可得:mg=2Fcos(90°-θ)
得:F=$\frac{mg}{2cos(90°-θ)}$=$\frac{mg}{2sinθ}$.
(2)因为力FAC与FAB的合力竖直向下,如图己所示,则有:$\frac{{F}_{AB}}{sinα}$=$\frac{{F}_{AC}}{sinβ}$
解得:FAC:FAB=sin β:sin α.
答:(1)石块侧面所受弹力的大小为$\frac{mg}{2sinθ}$;
(2)钢索AC、AB的拉力FAC与FAB之比应为sin β:sin α.
点评 (1)本题考查力的平衡和力的合成;运用共点力平衡条件可以结合合成法、分解法、正交分解法求解.
(2)本题关键将钢索AC、AB的拉力FAC、FAB进行合成,然后根据正弦定理列式分析;但是目前江苏等省份明确规定只考虑直角三角形的情况,题目较为冷僻.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.一弹簧原长10cm,一端固定,另一端悬挂1N重的砝码,此时弹簧长度是11cm.如果把3根这样的弹簧串接起来,在最下端也悬挂1N重的砝码,则此时三根弹簧的总长度L和一根弹簧的劲度系数k是( )
| A. | L=31cm,k=100N/m | B. | L=33cm,k=100N/m | C. | L=31cm,k=1N/m | D. | L=33cm,k=1N/m |
1.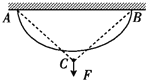 质量均匀、不可伸长的绳索两端分别系在天花板上的A、B两点,A、B两点间距离小于绳长,如图中实线所示.现在绳的中点C施加竖直向下的力F,将绳子缓慢拉直,如图中虚线所示,在此过程中( )
质量均匀、不可伸长的绳索两端分别系在天花板上的A、B两点,A、B两点间距离小于绳长,如图中实线所示.现在绳的中点C施加竖直向下的力F,将绳子缓慢拉直,如图中虚线所示,在此过程中( )
 质量均匀、不可伸长的绳索两端分别系在天花板上的A、B两点,A、B两点间距离小于绳长,如图中实线所示.现在绳的中点C施加竖直向下的力F,将绳子缓慢拉直,如图中虚线所示,在此过程中( )
质量均匀、不可伸长的绳索两端分别系在天花板上的A、B两点,A、B两点间距离小于绳长,如图中实线所示.现在绳的中点C施加竖直向下的力F,将绳子缓慢拉直,如图中虚线所示,在此过程中( )| A. | 绳的重心位置逐渐降低 | B. | 绳的重心位置始终不变 | ||
| C. | 绳的重力势能增大 | D. | 绳的重力势能减小 |
18.某物体同时受到同一平面内的三个共点力作用,在如图所示的四种情况中(坐标纸中每格边长表示1N大小的力),关于该物体所受的合力大小,下列说法正确的是( )
| A. |  图中物体所受的合力大小等于5 N | B. |  图中物体所受的合力大小等于2 N | ||
| C. |  图中物体所受的合力大小等于0 | D. |  图中物体所受的合力大小等于0 |
5.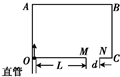 如图所示,在矩形OABC内有垂直于该矩形所在平面的匀强磁场(图中未画出),其下边OC是一个带有孔、缝的挡板.小孔O(大小不计)连着一根垂直于OC的直管,缝宽度为d,其左端M到孔的距离为L(d<<L),利用此装置可以选择一定速率范围内的电子.现有一束电子经直管从O点以不同的速率进入磁场,其中一部分电子从缝射出,对于此装置的分析,下列说法正确的是( )
如图所示,在矩形OABC内有垂直于该矩形所在平面的匀强磁场(图中未画出),其下边OC是一个带有孔、缝的挡板.小孔O(大小不计)连着一根垂直于OC的直管,缝宽度为d,其左端M到孔的距离为L(d<<L),利用此装置可以选择一定速率范围内的电子.现有一束电子经直管从O点以不同的速率进入磁场,其中一部分电子从缝射出,对于此装置的分析,下列说法正确的是( )
 如图所示,在矩形OABC内有垂直于该矩形所在平面的匀强磁场(图中未画出),其下边OC是一个带有孔、缝的挡板.小孔O(大小不计)连着一根垂直于OC的直管,缝宽度为d,其左端M到孔的距离为L(d<<L),利用此装置可以选择一定速率范围内的电子.现有一束电子经直管从O点以不同的速率进入磁场,其中一部分电子从缝射出,对于此装置的分析,下列说法正确的是( )
如图所示,在矩形OABC内有垂直于该矩形所在平面的匀强磁场(图中未画出),其下边OC是一个带有孔、缝的挡板.小孔O(大小不计)连着一根垂直于OC的直管,缝宽度为d,其左端M到孔的距离为L(d<<L),利用此装置可以选择一定速率范围内的电子.现有一束电子经直管从O点以不同的速率进入磁场,其中一部分电子从缝射出,对于此装置的分析,下列说法正确的是( )| A. | 所加磁场的方向应向里 | |
| B. | 从N点射出的电子在磁场中运动的时间比从M点射出的电子长 | |
| C. | 若要选择速率更大的粒子,则应减小磁感应强度 | |
| D. | 若要使选择的电子速率范围更小,则应增大缝宽d |
3.刻舟求剑的故事大家都很熟悉,我国还曾经发行过一套刻舟求剑的邮票.故事说的是楚国有人坐船渡河时,不慎把剑掉入江中,他在舟上刻下记号,说:“这是剑掉下的地方.”当舟停止时,他才沿着记号跳入河中找剑,遍寻不获.从运动学的角度来认识,下面说法正确的是( )


| A. | 楚人的错误在于把小船当做了质点 | |
| B. | 楚人的错误在于把小船的路程当做了位移 | |
| C. | 楚人的错误在于认为剑会随船一起运动 | |
| D. | 应选河岸或附近的相对河岸固定不动的物体做参考系 |
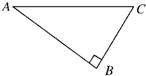 如图所示,A、B、C是匀强电场中的三点,已知φA=10V,φB=4V,φC=-2V,∠A=30°,∠B=90°,AC=$\sqrt{3}$cm,试确定该电场中的一根电场线和场强E的大小.
如图所示,A、B、C是匀强电场中的三点,已知φA=10V,φB=4V,φC=-2V,∠A=30°,∠B=90°,AC=$\sqrt{3}$cm,试确定该电场中的一根电场线和场强E的大小.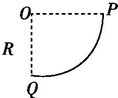 如图所示,竖直平面内固定有一个半径为R的四分之一圆弧轨道PQ,其中半径OP水平、OQ竖直,现从圆心O处以不同的初速度水平抛出一系列质量为m的相同小球,这些小球都落到了圆轨道上,不计空气阻力,重力加速度为g.
如图所示,竖直平面内固定有一个半径为R的四分之一圆弧轨道PQ,其中半径OP水平、OQ竖直,现从圆心O处以不同的初速度水平抛出一系列质量为m的相同小球,这些小球都落到了圆轨道上,不计空气阻力,重力加速度为g. 1935年在苏联的一条直铁轨上,有一列火车因蒸汽不足而停驶,驾驶员把货车厢甲(如图所示)留在现场,只拖着几节车厢向前方不远的车站开进,但他忘了将货车厢刹好,使车厢在斜坡上以4m/s的速度匀速后退,此时另一列火车乙正以16m/s的速度向该货车厢驶来.驾驶技术相当好的驾驶员波尔西列夫发现货车厢甲向自己驶来时两车相距仅100m,他立即刹车,紧接着加速倒退,结果恰好接住了货车厢甲,从而避免了相撞.设列车乙刹车过程和加速倒退过程均为匀变速直线运动,且加速度大小相等,求列车乙刹车和加速倒退过程的加速度大小.
1935年在苏联的一条直铁轨上,有一列火车因蒸汽不足而停驶,驾驶员把货车厢甲(如图所示)留在现场,只拖着几节车厢向前方不远的车站开进,但他忘了将货车厢刹好,使车厢在斜坡上以4m/s的速度匀速后退,此时另一列火车乙正以16m/s的速度向该货车厢驶来.驾驶技术相当好的驾驶员波尔西列夫发现货车厢甲向自己驶来时两车相距仅100m,他立即刹车,紧接着加速倒退,结果恰好接住了货车厢甲,从而避免了相撞.设列车乙刹车过程和加速倒退过程均为匀变速直线运动,且加速度大小相等,求列车乙刹车和加速倒退过程的加速度大小.