题目内容
8.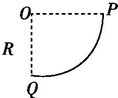 如图所示,竖直平面内固定有一个半径为R的四分之一圆弧轨道PQ,其中半径OP水平、OQ竖直,现从圆心O处以不同的初速度水平抛出一系列质量为m的相同小球,这些小球都落到了圆轨道上,不计空气阻力,重力加速度为g.
如图所示,竖直平面内固定有一个半径为R的四分之一圆弧轨道PQ,其中半径OP水平、OQ竖直,现从圆心O处以不同的初速度水平抛出一系列质量为m的相同小球,这些小球都落到了圆轨道上,不计空气阻力,重力加速度为g.(1)若小球从抛出到击中轨道所用时间为$\sqrt{\frac{R}{g}}$,求小球平抛的初速度v0.
(2)某同学认为初速度越小,则小球撞击轨道的动能越小;另一同学认为初速度越大,小球落到圆弧轨道时下降的高度越小,则小球撞击轨道的动能越小,请通过推理说明你的观点.
分析 小球做平抛运动,根据平抛运动的规律得到初速度;
根据动能定理得到小球落到圆弧上时的动能与下落高度的关系,再根据数学知识分析即可.
解答  解:(1)如图乙所示,对小球,有:
解:(1)如图乙所示,对小球,有:
竖直方向:y=$\frac{1}{2}$gt2=$\frac{1}{2}$R
水平方向x=$\sqrt{{R}^{2}-{y}^{2}}$=$\frac{\sqrt{3}}{2}$R
平抛的初速度v0=$\frac{x}{t}$=$\frac{\sqrt{3gR}}{2}$.
(2)设小球以初速度v抛出并撞到轨道上,根据动能定理得:
mgy'=Ek-$\frac{1}{2}$mv2
且x'=vt'
y'=$\frac{1}{2}$gt'2
x'2+y'2=R2
解得Ek=mg($\frac{3}{4}$y'+$\frac{{R}^{2}}{4y'}$)
当$\frac{3}{4}$y'=$\frac{{R}^{2}}{4y'}$,即y'=$\frac{\sqrt{3}}{3}$R时,小球撞击轨道的动能有最小值,Ek有最小值,在初速度不断增大的过程中,小球的动能先减小后增大.
综上所述,两位学生的观点都不正确.
答:(1)小球平抛的初速度v0为$\frac{\sqrt{3gR}}{2}$;
(2)两位学生的观点都不正确
点评 本题第二小问中采用数学上的函数法,得到动能与y的解析式,由数学不等式法分析动能的变化情况.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
6. 如图所示,AB为天花板,BC为竖直墙,用两轻绳OD、OE系一质量为m的小球,使之静止于O点,现保持小球位置不变,将水平绳OE的E端沿BC上移到B点的过程中,对两绳上的张力TD、TE的变化情况判断正确的是( )
如图所示,AB为天花板,BC为竖直墙,用两轻绳OD、OE系一质量为m的小球,使之静止于O点,现保持小球位置不变,将水平绳OE的E端沿BC上移到B点的过程中,对两绳上的张力TD、TE的变化情况判断正确的是( )
 如图所示,AB为天花板,BC为竖直墙,用两轻绳OD、OE系一质量为m的小球,使之静止于O点,现保持小球位置不变,将水平绳OE的E端沿BC上移到B点的过程中,对两绳上的张力TD、TE的变化情况判断正确的是( )
如图所示,AB为天花板,BC为竖直墙,用两轻绳OD、OE系一质量为m的小球,使之静止于O点,现保持小球位置不变,将水平绳OE的E端沿BC上移到B点的过程中,对两绳上的张力TD、TE的变化情况判断正确的是( )| A. | TD不断增大 | B. | TD不断减小 | C. | TE先增大后减小 | D. | TE先减小后增大 |
3. 如图所示,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过定滑轮(不计定滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A竖直下落、B沿斜面下滑,若以虚线所在处为零势能参考平面,下列说法正确的是( )
如图所示,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过定滑轮(不计定滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A竖直下落、B沿斜面下滑,若以虚线所在处为零势能参考平面,下列说法正确的是( )
 如图所示,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过定滑轮(不计定滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A竖直下落、B沿斜面下滑,若以虚线所在处为零势能参考平面,下列说法正确的是( )
如图所示,表面光滑的固定斜面顶端安装一定滑轮,小物块A、B用轻绳连接并跨过定滑轮(不计定滑轮的质量和摩擦).初始时刻,A、B处于同一高度并恰好处于静止状态.剪断轻绳后A竖直下落、B沿斜面下滑,若以虚线所在处为零势能参考平面,下列说法正确的是( )| A. | 两物块着地时的重力势能EpA<EpB | B. | 两物块着地前重力做功WA>WB | ||
| C. | 两物块着地时的动能EkA>EkB | D. | 两物块着地时的机械能EA=EB |
17.以“龙腾水舞新广州”为主题的2012年广州春节焰火晚会农历正月初一在珠江河段琶洲会展中心精彩上演.关于焰火在空中运动的过程,以下说法中正确的是( )
| A. | 焰火向上运动的速度越来越小,所以加速度越来越小 | |
| B. | 焰火向上运动的速度变化越来越慢,所以加速度一定越来越小 | |
| C. | 焰火的加速度不断减小,所以速度越来越小 | |
| D. | 某时刻焰火的速度为零,其加速度一定为零 |
18. 游乐场中的摩天轮转动时,游客坐在轿厢内随轮一起匀速转动.若摩天轮直径为100m,每25min转一圈.以下说法正确的是( )
游乐场中的摩天轮转动时,游客坐在轿厢内随轮一起匀速转动.若摩天轮直径为100m,每25min转一圈.以下说法正确的是( )
 游乐场中的摩天轮转动时,游客坐在轿厢内随轮一起匀速转动.若摩天轮直径为100m,每25min转一圈.以下说法正确的是( )
游乐场中的摩天轮转动时,游客坐在轿厢内随轮一起匀速转动.若摩天轮直径为100m,每25min转一圈.以下说法正确的是( )| A. | 轿厢角速度为$\frac{π}{750}$ rad/s | |
| B. | 轿厢线速度为$\frac{2π}{15}$ m/s | |
| C. | 轿厢向心加速度为$\frac{{π}^{2}}{11250}$ m/s2 | |
| D. | 质量为50 kg的游客的向心力为($\frac{π}{15}$)2 N |
 质量为M、长为L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g,不计空气影响.
质量为M、长为L的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软轻绳,绳上套着一质量为m的小铁环.已知重力加速度为g,不计空气影响.
 图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°斜向下.已知割草机重300N.
图中工人在推动一台割草机,施加的力大小为100N,方向与水平地面成30°斜向下.已知割草机重300N.