题目内容
4. 如图所示,质量为50kg的人站在与滑轮水平距离为3m处,通过定滑轮将质量为20kg的货物匀速提起,测得滑轮距离地面的高度为5m,人手臂离地面的高度为1m,不!计滑轮大小和摩擦,忽略细绳的重力,人脚与地面间的动摩擦因数为0.5,人的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则:
如图所示,质量为50kg的人站在与滑轮水平距离为3m处,通过定滑轮将质量为20kg的货物匀速提起,测得滑轮距离地面的高度为5m,人手臂离地面的高度为1m,不!计滑轮大小和摩擦,忽略细绳的重力,人脚与地面间的动摩擦因数为0.5,人的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.则:(1)地面对人的支持力和摩擦力分别多大?
(2)若人有足够大的拉力,他最多拉起多大质量的货物?
分析 (1)首先结合几何关系得到细线与水平方向的夹角,然后分别对重物和人受力分析,根据平衡条件列式求解;
(2)对人受力分析,受拉力、重力、支持力和静摩擦力,其中静摩擦力达到最大值,根据平衡条件并结合正交分解法列式求解即可.
解答 解:(1)细线与水平方向的夹角的正切值为:tanθ=$\frac{5m-1m}{3m}=\frac{4}{3}$,故θ=53°;
对重物分析,受重力和拉力而匀速上升,故拉力T=mg=200N;
再对人受力分析,受重力、拉力、支持力和静摩擦力,根据平衡条件,有:
N=Mg-Tsin53°=500-200×0.8=340N,
f=Tcos53°=200×0.6=120N;
(2)若人有足够大的拉力,临界情况是人与地面间的摩擦力等于最大静摩擦力,根据平衡条件,水平方向,有:Tcos53°-f=0,
竖直方向,有:Tsin53°+N=Mg,
其中:f=μN,T=mg
联立解得:
m=$\frac{μMg}{g(0.6+0.8μ)}=\frac{0.5×50×10}{10×(0.6+0.8×0.5)}=25kg$
答:(1)地面对人的支持力为340N,摩擦力为120N;
(2)若人有足够大的拉力,他最多拉起25kg质量的货物.
点评 本题关键是明确人的受力情况,根据平衡条件并采用正交分解法列式求解.
利用正交分解方法解体的一般步骤:
①明确研究对象;
②进行受力分析;
③建立直角坐标系,建立坐标系的原则是让尽可能多的力落在坐标轴上,将不在坐标轴上的力正交分解;
④x方向,y方向分别列平衡方程求解.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
14.一名观察者站在站台边,火车进站从他身边经过,火车共20节车厢,当第10节车厢完全经过他身边时,火车刚好停下.设火车做匀减速直线运动且每节车厢长度相同,则第7节和第8节车厢从他身边经过所用时间的比值为( )
| A. | $\sqrt{2}$:$\sqrt{3}$ | B. | ($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$) | C. | (2-$\sqrt{3}$):($\sqrt{3}$-$\sqrt{2}$) | D. | ($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1) |
15.下列物体的受力分析图正确的是( )
| A. |  静止在斜面上的小木块 | B. |  光滑接触面上静止的小球 | ||
| C. |  静止悬挂的小球 | D. |  静止在墙脚的杆 |
12.下列关于摩擦力的说法,正确的是( )
| A. | 相互接触并挤压的两物体间一定存在摩擦力 | |
| B. | 滑动摩擦力总是阻碍物体的运动 | |
| C. | 静止的物体也可以受到滑动摩擦力 | |
| D. | 只有静止的物体才受静摩擦力作用,运动的物体不会受静摩擦力作用 |
5.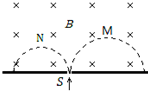 质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
 质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )| A. | M带正电,N带负电 | B. | M的速率大于N的速率 | ||
| C. | 洛仑兹力对M、N做正功 | D. | M、N的运行时间相等 |
 如图所示,真空中有两个等量异种点电荷A和B,一带负电的试探电荷仅受电场力作用,在电场中运动的部分轨迹如图中实线所示.M、N是轨迹上的两点,MN连线与AB连线垂直,O为垂足,且AO>OB.可以判断A一定带负电(正电或负电)
如图所示,真空中有两个等量异种点电荷A和B,一带负电的试探电荷仅受电场力作用,在电场中运动的部分轨迹如图中实线所示.M、N是轨迹上的两点,MN连线与AB连线垂直,O为垂足,且AO>OB.可以判断A一定带负电(正电或负电) 如图所示,在倾角为37°的斜面上,一个物体以20m/s的速度从A点向上滑行经2s到达最高点B而后折回,求:物体返回时的加速度?(g取10m/s2)
如图所示,在倾角为37°的斜面上,一个物体以20m/s的速度从A点向上滑行经2s到达最高点B而后折回,求:物体返回时的加速度?(g取10m/s2)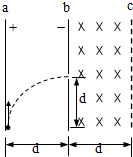 如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入匀强磁场,磁场区域bc的宽度也为d,磁感应强度方向垂直纸面向里,大小等于$\frac{E}{{v}_{0}}$.求微粒从射入电场到离开磁场所用的时间.
如图所示,竖直放置的两块很大的平行金属板a、b,相距为d,ab间的电场强度为E,今有一带正电的微粒从a板下缘以初速度v0竖直向上射入电场,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入匀强磁场,磁场区域bc的宽度也为d,磁感应强度方向垂直纸面向里,大小等于$\frac{E}{{v}_{0}}$.求微粒从射入电场到离开磁场所用的时间.