题目内容
8. 如图所示,重力为G的小球套在固定在竖直面内的半径为R的光滑的大圆环上,劲度为k的轻弹簧上端固定在大圆环的最高点,下端与小球相连,当小球静止时,弹簧处于伸长状态,与竖直方向间的夹角为θ=30°求
如图所示,重力为G的小球套在固定在竖直面内的半径为R的光滑的大圆环上,劲度为k的轻弹簧上端固定在大圆环的最高点,下端与小球相连,当小球静止时,弹簧处于伸长状态,与竖直方向间的夹角为θ=30°求(1)大圆环对小球弹力的大小F1;
(2)弹簧对小球拉力的大小F2;
(3)弹簧的原长.
分析 以小环为研究对象,分析受力情况,画出力图,根据平衡条件,运用三角形相似法求解即可.
解答 解:(1)选小环为研究对象,其受力情况如图所示,由于小环处于平衡状态;G,F1,F2三个力合力为零.可知弹簧处于拉伸状态.
由图可知,△AOB是等腰三角形,所以F1=G=mg,
(2)弹簧对小球拉力的大小:${F}_{2}=2mgcosθ=2mgcos30°=\sqrt{3}mg$
(3)受力如图所示,设弹簧与竖直方向夹角为θ.由几何关系可以看出OB与竖直方向之间的夹角是2θ,F1,F2夹角为180°-θ.
根据几何关系,有:$\frac{{F}_{2}}{sin2θ}=\frac{mg}{-sin(180°-θ)}$
由胡克定律,有F=k(2Rcosθ-L)
解得:L=$\sqrt{3}$R-$\frac{\sqrt{3}mg}{k}$
答:(1)大圆环对小球弹力的大小是mg;
(2)弹簧对小球拉力的大小是$\sqrt{3}$mg;
(3)弹簧的原长是$\sqrt{3}$R-$\frac{\sqrt{3}mg}{k}$.
点评 对于涉及非直角三角形的力平衡问题,可以运用三角相似法处理,也可以运用三角函数法研究.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
 如图所示在光滑、绝缘的水平面上,沿一直线依次排列三个带电小球A、B、C(可视为质点).若它们恰能处于平衡状态.那么这三个小球所带的电荷量及电性的关系,下面的情况可能的是( )
如图所示在光滑、绝缘的水平面上,沿一直线依次排列三个带电小球A、B、C(可视为质点).若它们恰能处于平衡状态.那么这三个小球所带的电荷量及电性的关系,下面的情况可能的是( ) 如图所示,长度为L=6m、质量M=4kg的长木板置于光滑的水平面上,其左端有一大小可忽略、质量m=1kg的物块,物块与木板间的动摩擦因数为0.4,开始时物块与木板都处于静止状态,现对物块施加一方向水平向右的恒定拉力,设最大静摩擦力等于滑动摩擦力,(g=10m/s2),求:
如图所示,长度为L=6m、质量M=4kg的长木板置于光滑的水平面上,其左端有一大小可忽略、质量m=1kg的物块,物块与木板间的动摩擦因数为0.4,开始时物块与木板都处于静止状态,现对物块施加一方向水平向右的恒定拉力,设最大静摩擦力等于滑动摩擦力,(g=10m/s2),求: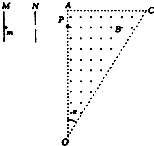 如图所示,直角三角形OAC(a=30°)区域内有B=0.5T的匀强磁场,方向如图所示.两平行极板M、N接在电压为u的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为$\frac{q}{m}$=105C/kg,OP间距离为L=0.3m.全过程不计粒子所受的重力,则:
如图所示,直角三角形OAC(a=30°)区域内有B=0.5T的匀强磁场,方向如图所示.两平行极板M、N接在电压为u的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为$\frac{q}{m}$=105C/kg,OP间距离为L=0.3m.全过程不计粒子所受的重力,则: 如图所示,有一个100匝的线圈,其横截面的边长为L=0.20m的正方形,放在磁感应强度为B=0.50T的匀强磁场中,线圈平面与磁场垂直.若将这个线圈横截面的形状由正方形改变成圆形(横截面的周长不变),在这一过程中穿过线圈的磁通量改变了多少?
如图所示,有一个100匝的线圈,其横截面的边长为L=0.20m的正方形,放在磁感应强度为B=0.50T的匀强磁场中,线圈平面与磁场垂直.若将这个线圈横截面的形状由正方形改变成圆形(横截面的周长不变),在这一过程中穿过线圈的磁通量改变了多少?
 如图所示,A、B质量分别力m1=lkg,m2=2kg.置于小车C上,小车质量m3=1kg,A、B间粘有少量炸药,A、B与小车间的动摩擦因素均为0.5,小车静止在光滑水平面上.若炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能.A、B始终在小车表面上水平运动,求:
如图所示,A、B质量分别力m1=lkg,m2=2kg.置于小车C上,小车质量m3=1kg,A、B间粘有少量炸药,A、B与小车间的动摩擦因素均为0.5,小车静止在光滑水平面上.若炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能.A、B始终在小车表面上水平运动,求: