题目内容
4.某质量为m的卫星绕地球做匀速圆周运动,其轨道离地面的高度等于地球的半径R,已知地球表面的重力加速度为g,忽略地球的自转效应,则( )| A. | 卫星的绕行速度大小为$\frac{1}{2}$$\sqrt{gR}$ | |
| B. | 卫星的绕行周期大小为2π$\sqrt{\frac{2R}{g}}$ | |
| C. | 卫星所在处的重力加速度大小为$\frac{1}{2}$g | |
| D. | 卫星的动能大小为$\frac{1}{4}$mgR |
分析 卫星绕地球做匀速圆周运动,由万有引力提供向心力,在地球表面,万有引力等于物体的重力,根据牛顿第二定律和圆周运动公式即可求解.
解答 解:A、根据万有引力提供向心力有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$,得$v=\sqrt{\frac{GM}{r}}$,地球表面物体重力等于万有引力$mg=G\frac{Mm}{{R}_{\;}^{2}}$,得$GM=g{R}_{\;}^{2}$,卫星的轨道半径r=2R,所以有$v=\sqrt{\frac{g{R}_{\;}^{2}}{2R}}=\sqrt{\frac{gR}{2}}$,故A错误;
B、根据万有引力提供向心力有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$得$T=\sqrt{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{GM}}$=$\sqrt{\frac{4{π}_{\;}^{2}(2R)_{\;}^{3}}{g{R}_{\;}^{2}}}$=$2π\sqrt{\frac{8R}{g}}$,故B错误;
C、根据万有引力等于重力$mg′=G\frac{Mm}{(2R)_{\;}^{2}}$得$g′=G\frac{M}{4{R}_{\;}^{2}}=\frac{g{R}_{\;}^{2}}{4{R}_{\;}^{2}}=\frac{g}{4}$,故C错误;
D、由A得到$v=\sqrt{\frac{gR}{2}}$,卫星的动能${E}_{k}^{\;}=\frac{1}{2}m{v}_{\;}^{2}=\frac{1}{2}m\frac{gR}{2}=\frac{1}{4}mgR$,故D正确
故选:D
点评 该题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,解题过程中要注意黄金代换式$GM=g{R}_{\;}^{2}$的应用.

 如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )
如图所示,在有活塞的气缸中密闭着一定质量的理想气体,将一个半导体热敏电阻(阻值随温度的升高而减小)R置于气缸中,气缸固定不动,缸内活塞可以自由移动且不漏气,活塞下挂一沙桶,沙桶装满沙子时活塞恰好能够静止.热敏电阻R与汽缸外的电源E和灵敏电流表A组成闭合回路,气缸和活塞具有良好的绝热性能.如果在沙桶的底部钻上一个小孔,那么在细沙缓缓漏出的过程中,以下判断正确的是( )| A. | 气体内能将一定增大 | B. | 气体压强将一定减小 | ||
| C. | 气体将一定对外做功 | D. | 电流表的示数将变小 |
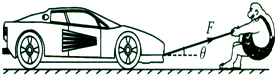 漫画中的大力士用绳子拉动汽车,绳中的拉力为F,绳与水平方向的夹角为θ.若将F沿水平和竖直方向分解,则其竖直方向的分力为( )
漫画中的大力士用绳子拉动汽车,绳中的拉力为F,绳与水平方向的夹角为θ.若将F沿水平和竖直方向分解,则其竖直方向的分力为( )| A. | Fsinθ | B. | Fcosθ | C. | $\frac{F}{sinθ}$ | D. | $\frac{F}{cosθ}$ |
 如图是观察水波衍射的实验装置.AB和CD是两块挡板,BC是两块挡板之间的空隙,O为水波的波源,图中已画出波源附近区域波的传播情况,实线波纹表示波峰.关于水波经过BC空隙之后的传播情况,下列说法中正确的是( )
如图是观察水波衍射的实验装置.AB和CD是两块挡板,BC是两块挡板之间的空隙,O为水波的波源,图中已画出波源附近区域波的传播情况,实线波纹表示波峰.关于水波经过BC空隙之后的传播情况,下列说法中正确的是( )| A. | 观察不到明显的衍射现象 | |
| B. | 水波经过空隙BC后波纹间距变小 | |
| C. | 若保持波源的频率不变,而增大空隙BC的宽度,有可能观察不到明显的衍射现象 | |
| D. | 若保持空隙BC的宽度不变,而增大波源的频率,可以观察到更加明显的衍射现象 |

| A. | 受重力、支持力和静摩擦力的作用 | B. | 受重力、支持力和向心力的作用 | ||
| C. | 静摩擦力的方向与运动方向相反 | D. | 重力和支持力是一对相互作用力 |

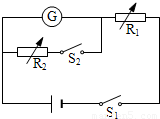 在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材:
在把一个2mA电流表改装成电压表的实验中,测定电流表的内阻时,备有如下器材: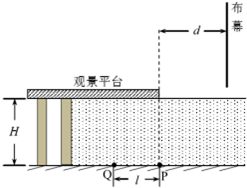 一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求: