题目内容
9. 如图所示,为一磁约束装置的原理图,同心圆内存在有垂直圆平面的匀强磁场,同心圆圆心O与xOy平面坐标系原点重合.半径为R0的圆形区域Ⅰ内有方向垂直xOy平面向里的匀强磁场B1.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(0、R0)的A点沿y轴负方向射入磁场区域Ⅰ,粒子全部经过x轴上的P点,方向沿x轴正方向.当在环形区域Ⅱ加上方向垂直于xOy平面的匀强磁场B2时,上述粒子仍从A点沿y轴负方向射入区域Ⅰ,粒子恰好能够约束在环形区域内,且经过环形区域Ⅱ后能够从Q点沿半径方向射入区域Ⅰ,已知OQ与x轴正方向成60°.不计重力和粒子间的相互作用.求:
如图所示,为一磁约束装置的原理图,同心圆内存在有垂直圆平面的匀强磁场,同心圆圆心O与xOy平面坐标系原点重合.半径为R0的圆形区域Ⅰ内有方向垂直xOy平面向里的匀强磁场B1.一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(0、R0)的A点沿y轴负方向射入磁场区域Ⅰ,粒子全部经过x轴上的P点,方向沿x轴正方向.当在环形区域Ⅱ加上方向垂直于xOy平面的匀强磁场B2时,上述粒子仍从A点沿y轴负方向射入区域Ⅰ,粒子恰好能够约束在环形区域内,且经过环形区域Ⅱ后能够从Q点沿半径方向射入区域Ⅰ,已知OQ与x轴正方向成60°.不计重力和粒子间的相互作用.求:(1)区域Ⅰ中磁感应强度B1的大小;
(2)环形区域Ⅱ中B2的大小、方向及环形外圆半径R的大小;
(3)粒子从A点沿y轴负方向射入后至第一次到Q点的运动时间.
分析 (1)粒子在区域Ⅰ中做匀速圆周运动,根据几何关系求半径,根据牛顿第二定律及动能定义式联立列式
(2)画出粒子在区域Ⅱ中的轨迹,根据几何关系求半径,根据牛顿第二定律求${B}_{2}^{\;}$,由左手定则求磁场方向
(3)求出轨迹所对的圆心角,根据$t=\frac{θ}{360}T$求出时间
解答 解: (1)设在区域Ⅰ内轨迹圆半径为r1,
(1)设在区域Ⅰ内轨迹圆半径为r1,
则 r1=R0
根据牛顿第二定律:$qv{B_1}=m\frac{v^2}{r_1}$
动能的定义:${E}_{0}^{\;}=\frac{1}{2}m{v}_{\;}^{2}$
${B}_{1}^{\;}=\frac{\sqrt{2m{E}_{0}^{\;}}}{q{R}_{0}^{\;}}$
(2)设粒子在区域Ⅱ中的轨迹圆半径为${r}_{2}^{\;}$,部分轨迹如图,有几何关系知
${r}_{2}^{\;}=\frac{\sqrt{3}}{3}{r}_{1}^{\;}$
根据牛顿第二定律:$qv{B_2}=m\frac{v^2}{r_2}$
${B}_{2}^{\;}$=$\frac{\sqrt{6m{E}_{0}^{\;}}}{q{R}_{0}^{\;}}$
方向与${B}_{1}^{\;}$相反,即垂直xOy平面向外
由几何关系得$R=\frac{r_2}{sin30°}+{r_2}=3{r_2}$,
即$R=\sqrt{3}{R}_{0}^{\;}$
(3)由题意可知 $t=(\frac{1}{4}{T_1}+\frac{2}{3}{T_2})$
${T}_{1}^{\;}=\frac{2πm}{q{B}_{1}^{\;}}$,${T}_{2}^{\;}=\frac{2πm}{q{B}_{2}^{\;}}$
代入数据得$t=(\frac{{2\sqrt{6}}}{9}+\frac{{\sqrt{2}}}{4})•\frac{{π{R_0}\sqrt{m{E_0}}}}{E_0}$
答:(1)区域Ⅰ中磁感应强度B1的大小$\frac{\sqrt{2m{E}_{0}^{\;}}}{q{R}_{0}^{\;}}$;
(2)环形区域Ⅱ中B2的大小$\frac{\sqrt{6m{E}_{0}^{\;}}}{q{R}_{0}^{\;}}$、方向与${B}_{1}^{\;}$相反,即垂直xoy平面向外,及环形外圆半径R的大小$\sqrt{3}{R}_{0}^{\;}$;
(3)粒子从A点沿y轴负方向射入后至第一次到Q点的运动时间$(\frac{2\sqrt{6}}{9}+\frac{\sqrt{2}}{4})•\frac{π{R}_{0}^{\;}\sqrt{m{E}_{0}^{\;}}}{{E}_{0}^{\;}}$.
点评 该题考查带电粒子在磁场中的运动,解决本题的关键掌握带电粒子在有界磁场中做匀速圆周运动时,如何确定圆心、半径.

 阅读快车系列答案
阅读快车系列答案
| A. | P、Q是两个等量正电荷 | B. | P、Q是两个等量负电荷 | ||
| C. | P、Q是两个不等量异种电荷 | D. | P、Q是两个等量异种电荷 |
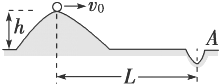 2011年8月深圳大运会高尔夫球女子团体比赛中,中华台北队获两枚金牌,中国女队队员黎佳韵在个人赛中也有不俗表现.随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图4-2-24所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )
2011年8月深圳大运会高尔夫球女子团体比赛中,中华台北队获两枚金牌,中国女队队员黎佳韵在个人赛中也有不俗表现.随着人们生活水平的提高,高尔夫球将逐渐成为普通人的休闲娱乐.如图4-2-24所示,某人从高出水平地面h的坡上水平击出一个质量为m的高尔夫球.由于恒定的水平风力的作用,高尔夫球竖直落入距击球点水平距离为L的A穴.则( )| A. | 球被击出后做平抛运动 | |
| B. | 该球从被击出到落入A穴所用的时间为$\sqrt{\frac{2h}{g}}$ | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2g}{h}}$ | |
| D. | 球被击出后受到的水平风力的大小为$\frac{mgh}{L}$ |

| A. | a质点振动减弱 | B. | b质点振动加强,一直处于波峰 | ||
| C. | c质点振动加强,一直处于波谷 | D. | d质点振动减弱 |
| A. | 物体作曲线运动时,它的速度可能保持不变 | |
| B. | 物体只有受到一个方向不断改变的力的作用,才可能作曲线运动 | |
| C. | 所有作曲线运动的物体,所受合外力方向与速度方向肯定不在一条直线上 | |
| D. | 所有作曲线运动的物体,加速度方向与所受合外力方向始终不一致 |


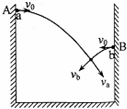 如图所示,将a、b两小球均以大小为20m/s的初速度分别从A、B两点间隔3s先后水平相向抛出,两小球恰好在空中相遇,且相遇时速度方向相互垂直,不计空气阻力,取g=10m/s2,则抛出点A、B间的水平距离是( )
如图所示,将a、b两小球均以大小为20m/s的初速度分别从A、B两点间隔3s先后水平相向抛出,两小球恰好在空中相遇,且相遇时速度方向相互垂直,不计空气阻力,取g=10m/s2,则抛出点A、B间的水平距离是( )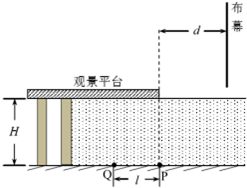 一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=4m,在距观景平台右侧边缘正前方d=4m处有垂直湖面足够大的宣传布幕.在P点左侧l=3m处湖底上的Q点安装有一单色光光源(可视为点光源).已知水对该单色光的折射率n=$\frac{4}{3}$,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求: