题目内容
18.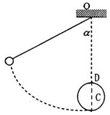 长为L的轻绳一端系一小球(可视为质点),另一端悬于O点.小球从与竖直方向成60°角处释放,到最低点与一钉子C相碰后绕C做圆周运动,欲使小球刚好能通过最高点,则钉子距悬点O的距离h为多大.(不计空气阻力)
长为L的轻绳一端系一小球(可视为质点),另一端悬于O点.小球从与竖直方向成60°角处释放,到最低点与一钉子C相碰后绕C做圆周运动,欲使小球刚好能通过最高点,则钉子距悬点O的距离h为多大.(不计空气阻力)
分析 对小球从静止到D的运动过程应用机械能守恒求得速度,然后由牛顿第二定律求得在D点的速度,联立两速度即可求解.
解答 解:小球运动到最低点的过程只有重力做功,那么由机械能守恒可得:$mgL(1-cos60°)=\frac{1}{2}m{v}^{2}$;
小球从最低点到D的运动过程,只有重力做功,那么由机械能守恒可得:$\frac{1}{2}m{v}^{2}=2mg(L-h)+\frac{1}{2}m{{v}_{D}}^{2}$;
小球刚好能通过最高点D,故由牛顿第二定律可得:$mg=\frac{m{{v}_{D}}^{2}}{L-h}$;
所以,$mgL(1-cos60°)=2mg(L-h)+\frac{1}{2}mg(L-h)$=$\frac{5}{2}mg(L-h)$,所以,$h=\frac{4}{5}L$;
答:欲使小球刚好能通过最高点,则钉子距悬点O的距离h为$\frac{4}{5}L$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.2007年度诺贝尔物理学奖授予了法国和德国的两位科学家,以表彰他们发现“巨磁电阻效应”.巨磁电阻效应的发现,使得影响材料电阻率的因数就变成:温度、材料、光强和磁场等.基于巨磁开发的用于读取硬盘数据的技术,被认为是纳米技术的第一次真正应用.在下列有关其它电阻应用的说法中.正确的是( )
| A. | 光敏电阻是一种光电传感器 | |
| B. | 热敏电阻可应用于电热设备中,以用来发热 | |
| C. | 应用于电炉、电阻器等设备中的电阻丝一般选用单质金属材料来做 | |
| D. | 电阻在电路中的主要作用是:通直流、阻交流 |
12.A、B两个物体(可看做质点)间的万有引力大小为F,若B物质的质量增加到原来的两倍,A物体的质量不变,同时使它们之间的距离减为原来的一半,则A、B两物体万有引力的大小将变为( )
| A. | F | B. | $\frac{F}{2}$ | C. | 4F | D. | 8F |
7. 如图所示,是两个不同电阻的I-U图象,则图线①、②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )
如图所示,是两个不同电阻的I-U图象,则图线①、②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )
 如图所示,是两个不同电阻的I-U图象,则图线①、②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )
如图所示,是两个不同电阻的I-U图象,则图线①、②表示的电阻及两电阻串联或并联后的I-U图象所在区域分别是( )| A. | ①表示电阻大的图象,串联后在区域I | |
| B. | ①表示电阻小的图象,并联后在区域II | |
| C. | ②表示电阻大的图象,并联后在区域II | |
| D. | ②表示电阻大的图象,串联后在区域III |
4. 真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )
真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )
 真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )
真空中有一个正方体区域abfe-dcgh,有一对等量异种点电荷分别位于正方体的顶点a和f处,现在各顶点间移动一正试探电荷,关于该试探电荷所受的电场力和具有的电势能,以下判断正确的是( )| A. | 在d点和g点所受电场力大小相等、方向相同 | |
| B. | 在h点和c点所受电场力大小相等、方向相同 | |
| C. | 在d点和g点电势能相等 | |
| D. | 在h点和c点电势能相等 |
 如图所示,竖直平面内的$\frac{3}{4}$圆弧形光滑管道的半径略大于小球半径,管道的半径为R,A端与圆心O等高,AD为水平面,B点在O点的正下方,质量为m小球自A点正上方距圆弧顶端2R处由静止释放,自由下落至A点时进入管道,从上端口飞出后落在C点.则小球在从开始经A、B最后落到C点的过程中,重力做的功为3mgR;小球从圆弧上端飞出最后落到C点所用的时间为$\sqrt{\frac{2R}{g}}$.
如图所示,竖直平面内的$\frac{3}{4}$圆弧形光滑管道的半径略大于小球半径,管道的半径为R,A端与圆心O等高,AD为水平面,B点在O点的正下方,质量为m小球自A点正上方距圆弧顶端2R处由静止释放,自由下落至A点时进入管道,从上端口飞出后落在C点.则小球在从开始经A、B最后落到C点的过程中,重力做的功为3mgR;小球从圆弧上端飞出最后落到C点所用的时间为$\sqrt{\frac{2R}{g}}$. 如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3s后又恰好垂直与倾角为45°的斜面相碰.已知半圆形管道的半径为R=1m,小球可看作质点且其质量为m=1kg,g取10m/s2.求:
如图所示,一个固定在竖直平面上的光滑半圆形管道,管道里有一个直径略小于管道内径的小球,小球在管道内做圆周运动,从B点脱离后做平抛运动,经过0.3s后又恰好垂直与倾角为45°的斜面相碰.已知半圆形管道的半径为R=1m,小球可看作质点且其质量为m=1kg,g取10m/s2.求: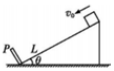 足够长的倾角为θ的粗糙斜面上,有一质量为m的滑块距挡板P为L,以初速度v0沿斜面下滑,并与挡板发生碰撞,滑块与斜面动摩擦因数为μ,μ<tanθ.若滑块与挡板碰撞没有机械能损失,求:
足够长的倾角为θ的粗糙斜面上,有一质量为m的滑块距挡板P为L,以初速度v0沿斜面下滑,并与挡板发生碰撞,滑块与斜面动摩擦因数为μ,μ<tanθ.若滑块与挡板碰撞没有机械能损失,求: