题目内容
1.若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )| A. | 月球表面的重力加速度g月=$\frac{2h{{v}_{0}}^{2}}{{L}^{2}}$ | |
| B. | 月球的平均密度ρ=$\frac{3h{{v}_{0}}^{2}}{2πG{L}^{2}R}$ | |
| C. | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2h}$ | |
| D. | 月球的质量m月=$\frac{2h{R}^{2}{{v}_{0}}^{2}}{G{L}^{2}}$ |
分析 宇航员在月球上自高h处以初速度v0水平抛出一物体,测出物体的水平射程为L,根据水平射程和初速度求出运动的时间,根据h=$\frac{1}{2}$gt2求出月球表面的重力加速度大小;由$g=\frac{Gm}{{r}^{2}}$求得月球的质量;根据重力提供向心力求出卫星的第一宇宙速度;由质量与半径可求得平均密度.
解答 解:A、平抛运动的时间t=$\frac{L}{{v}_{0}}$.再根据h=$\frac{1}{2}$gt2得,得${g_月}=\frac{2hv_0^2}{L^2}$,故A正确
B、月球的平均密度$ρ=\frac{{m}_{月}}{\frac{4}{3}π{R}^{3}}$=$\frac{3h{{v}_{0}}^{2}}{2πGR{L}^{2}}$,故B正确.
C、第一宇宙速度:$v=\sqrt{{g}_{月}R}=\sqrt{\frac{2h{v}_{0}^{2}}{{L}^{2}}R}$=$v=\frac{{v}_{0}}{L}\sqrt{2hR}$,故C错误
D、由${g}_{月}=\frac{G{m}_{月}}{{R}^{2}}$与${g}_{月}=\frac{2h{v}_{0}^{2}}{{L}^{2}}$,可得:m月=$\frac{2h{R}^{2}{v}_{0}^{2}}{G{L}^{2}}$.故D正确
故选:ABD
点评 解决本题的关键知道平抛运动在水平方向上和竖直方向上的运动规律,以及掌握万有引力提供向心力以及万有引力等于重力这两个理论的运用

练习册系列答案
相关题目
11.如图甲,矩形金属线框绕与磁感线垂直的转轴在匀强磁场中匀速转动,产生的交变电流经理想变压器给负载供电.原线圈两端的交变电压随时间变化的图象如图乙.电压表和电流表均为理想电表,Rt为阻值随温度升高而变小的热敏电阻,R1为定值电阻.则( )


| A. | t=0.005s时,电压表读数为0 | |
| B. | t=0.005s时,穿过线框回路的磁通量为零 | |
| C. | 金属线框的转速为50r/s | |
| D. | Rt温度升高时,变压器的输入功率变小 |
13.科学家设想在太空设立太阳能卫星电站,卫星电站的最佳位置是在赤道上空1100km的圆轨道上,那么此卫星电站比近地表面附近圆轨道上的卫星( )
| A. | 线速度大 | B. | 角速度大 | C. | 周期大 | D. | 向心加速度大 |

 某同学在“用单摆测重力加速度”的实验中,把摆球用细线悬挂在铁架台上,测量摆线长摆球直径,通过计算得到摆长L.
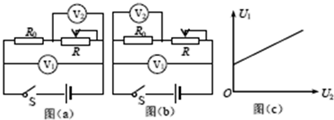
某同学在“用单摆测重力加速度”的实验中,把摆球用细线悬挂在铁架台上,测量摆线长摆球直径,通过计算得到摆长L. 某研究性学习小组探究小灯泡灯丝电阻与温度的关系,主要仪器有:
某研究性学习小组探究小灯泡灯丝电阻与温度的关系,主要仪器有: