题目内容
11．如图所示的皮带传动装置中，A、B、C分别是三个轮边缘上的点，A、B两点所在的轮同轴，B、C两轮用皮带连接且不打滑，rA：rB：rC=2：1：2，则A、B、C三点的线速度之比2：1：1；向心加速度之比4：2：1．
分析 两轮是皮带传动，皮带传动的特点是皮带和轮子接触点的线速度的大小相同，同轴传动角速度相同，然后利用v=ωr和向心加速度公式a=vω求解．
解答 解：由于B轮和C轮是皮带传动，皮带传动的特点是两轮与皮带接触点的线速度的大小与皮带的线速度大小相同，
故vC=vB，所以vB：vC=1：1
由于A轮和B轮共轴，故两轮角速度相同，即ωA=ωB，故ωA：ωB=1：1
由角速度和线速度的关系式v=ωR可得ωB：ωC=2：1
以上可知：
VA：VB：Vc=2：1：1
ωA：ωB：ωC=2：2：1，
根据a=ωv
结合ABC三点的线速度与和ABC三点的角速度比可得：aA：aB：aC=4：2：1
故答案为：2：1：1；4：2：1
点评 解决传动类问题要分清是摩擦传动（包括皮带传动，链传动，齿轮传动，线速度大小相同）还是轴传动（角速度相同）；灵活应用v=ωr和向心加速度求解．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
1．若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球，测出小球的水平射程为L．已知月球半径为R，万有引力常量为G．则下列说法正确的是（ ）
| A． | 月球表面的重力加速度g月=$\frac{2h{{v}_{0}}^{2}}{{L}^{2}}$ | |
| B． | 月球的平均密度ρ=$\frac{3h{{v}_{0}}^{2}}{2πG{L}^{2}R}$ | |
| C． | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2h}$ | |
| D． | 月球的质量m月=$\frac{2h{R}^{2}{{v}_{0}}^{2}}{G{L}^{2}}$ |
2．
如图所示，在固定斜面上有两个完全相同的小球a和b，两球从顶端滑到底端，a球由静止开始下滑，b球以水平速度v0紧贴斜面抛出，则下列说法中正确的是（ ）
如图所示，在固定斜面上有两个完全相同的小球a和b，两球从顶端滑到底端，a球由静止开始下滑，b球以水平速度v0紧贴斜面抛出，则下列说法中正确的是（ ）| A． | 若斜面光滑，a、b两球滑到底端所用的时间ta=tb | |
| B． | 若斜面光滑，a、b两球滑到底端时重力的功率相同 | |
| C． | 若斜面粗糙，a、b两球滑到底端所用的时间ta＞tb | |
| D． | 若斜面粗糙，a、b两球滑到底端所用的时间ta＜tb |
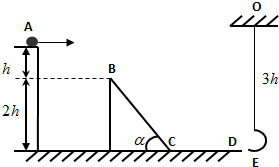如图所示，平台上的小球从A点水平抛出，恰好能无碰撞地进入光滑斜面BC，经C点进入光滑水平面CD时速率不变，最后进入悬挂在O点并与水平面等髙的弧形轻质筐内．己知小球质量为1kg，A、B两点髙度差为2m，斜面BC髙为4m，倾角a=45°，悬挂弧筐的轻绳长为6m，小球可以看成质点，轻质筐的重量忽略不计，弧形轻质筐的大小远小于悬线长度，重力加速度为g=10m/s2．求：
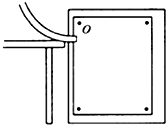（1）“探究平抛物体的运动规律”实验的装置如图所示，让小球多次沿同一轨道运动，通过描点法画小球做平抛运动的轨迹．为了能较准确地描绘运动轨迹，下面列出了一些操作要求，将你认为正确的选项前面的字母填在横线上：ACE．
石墨烯是近些年发现的一种新材料，其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化，其发现者由此获得2010年诺贝尔物理学奖．用石墨烯制作超级缆绳，人类搭建“太空电梯”的梦想有望在本世纪实现．科学家们设想，通过地球同步轨道站向地面垂下一条缆绳至赤道基站，电梯仓沿着这条缆绳运行，实现外太空和地球之间便捷的物资交换．
20．
2013年12月2日，我国探月卫星“嫦娥三号”在西昌卫星发射中心成功发射升空，飞行轨道示意图如图所示，卫星从地面发射后奔向月球，现在圆形轨道Ⅰ上运行，在P点从轨道Ⅰ进入椭圆轨道Ⅱ，Q为轨道Ⅱ上的近月点，则“嫦娥三号”在轨道Ⅱ上（ ）
2013年12月2日，我国探月卫星“嫦娥三号”在西昌卫星发射中心成功发射升空，飞行轨道示意图如图所示，卫星从地面发射后奔向月球，现在圆形轨道Ⅰ上运行，在P点从轨道Ⅰ进入椭圆轨道Ⅱ，Q为轨道Ⅱ上的近月点，则“嫦娥三号”在轨道Ⅱ上（ ）| A． | 运行的周期大于在轨道Ⅰ上运行的周期 | |
| B． | 从P到Q的过程中速率保持不变 | |
| C． | 经过P的速度小于在轨道Ⅰ上经过P的速度 | |
| D． | 经过P的加速度大于在轨道Ⅰ上经过P的加速度 |
