题目内容
9.如图所示,一端固定的弹簧被质量为m的小球紧压在粗糙水平轨道AB上,AB长为5r,动摩擦因数为μ,AB与半径为r的光滑半圆轨道BC相切.某一时刻,弹簧释放,小球由AB冲上BC,经最高点C平抛落到A、B间的某一点D,已知B、D间的距离为4r,重力加速度为g,求:
(1)小球在C点的速度大小;
(2)小球在C点时,轨道对小球的支持力.
分析 (1)小球离开C点后做平抛运动,已知平抛运动的竖直高度和水平位移,由分位移公式求解小球在C点的速度大小.
(2)小球在C点时,由重力和轨道的支持力的合力提供向心力,由牛顿第二定律求解.
解答 解:(1)小球离开C点后做平抛运动,由平抛运动的规律得
2r=$\frac{1}{2}g{t}^{2}$
4r=vCt
联立解得 vC=2$\sqrt{gr}$
(2)小球在C点时,由重力和轨道的支持力的合力提供向心力,由牛顿第二定律得
mg+N=m$\frac{{v}_{C}^{2}}{r}$
解得 N=3mg
答:
(1)小球在C点的速度大小是2$\sqrt{gr}$;
(2)小球在C点时,轨道对小球的支持力是3mg.
点评 本题的关键要分析清楚小球的运动过程,掌握平抛运动分运动的规律,明确圆周运动向心力的来源.

练习册系列答案
相关题目
20.一些问题你可能不会求解,但是你仍有可能对这些问题的解是否合理进行分析和判断.例如从解的物理量单位,解随某些已知量变化的趋势,从而判断解的合理性或正确性.举例如下:声音在空气中的传播速度v与空气的密度ρ、压强P有关.下列速度表达式中,k为比例系数,无单位,则这四个表达式中可能正确的是( )
| A. | v=k$\frac{P}{ρ}$ | B. | v=$\sqrt{\frac{kP}{ρ}}$ | C. | v=$\sqrt{\frac{kρ}{P}}$ | D. | v=$\sqrt{kPρ}$ |
14.许多光现象在科学技术上得到了应用,以下对一些应用的解释,正确的是( )
| A. | 紫外验钞机是利用了紫外线的化学作用 | |
| B. | X光透视利用的是光的干涉现象 | |
| C. | 工业上的金属探伤利用的是γ射线具有较强的衍射 | |
| D. | 红外遥感技术利用了一切物体都不停地辐射红外线的现象 |
1.若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
| A. | 月球表面的重力加速度g月=$\frac{2h{{v}_{0}}^{2}}{{L}^{2}}$ | |
| B. | 月球的平均密度ρ=$\frac{3h{{v}_{0}}^{2}}{2πG{L}^{2}R}$ | |
| C. | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2h}$ | |
| D. | 月球的质量m月=$\frac{2h{R}^{2}{{v}_{0}}^{2}}{G{L}^{2}}$ |
18.下列说法不符合物理学史的是( )
| A. | 奥斯特发现了电流的磁效应 | B. | 赫兹预言光也是电磁波 | ||
| C. | 法拉第发现了电磁感应现象 | D. | 伦琴首次发现了X射线 |
 物理兴趣小组要测量一电动车电池的电动势和内阻.已知该电池电动势为10~12V,实验室备有下列器材:
物理兴趣小组要测量一电动车电池的电动势和内阻.已知该电池电动势为10~12V,实验室备有下列器材: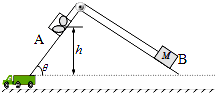 如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的光滑斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,g取10m/s2,sin53°=0.8,cos53°=0.6.
如图所示为仓储公司常采用的“自动化”货物装卸装置,两个相互垂直的光滑斜面固定在地面上,货箱A(含货物)和配重B通过与斜面平行的轻绳跨过光滑滑轮相连.A装载货物后从h=8.0m高处由静止释放,运动到底端时,A和B同时被锁定,卸货后解除锁定,A在B的牵引下被拉回原高度处,再次被锁定.已知θ=53°,B的质量M为1.0×103kg,g取10m/s2,sin53°=0.8,cos53°=0.6.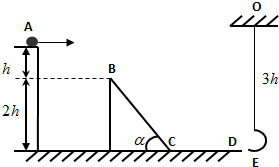 如图所示,平台上的小球从A点水平抛出,恰好能无碰撞地进入光滑斜面BC,经C点进入光滑水平面CD时速率不变,最后进入悬挂在O点并与水平面等髙的弧形轻质筐内.己知小球质量为1kg,A、B两点髙度差为2m,斜面BC髙为4m,倾角a=45°,悬挂弧筐的轻绳长为6m,小球可以看成质点,轻质筐的重量忽略不计,弧形轻质筐的大小远小于悬线长度,重力加速度为g=10m/s2.求:
如图所示,平台上的小球从A点水平抛出,恰好能无碰撞地进入光滑斜面BC,经C点进入光滑水平面CD时速率不变,最后进入悬挂在O点并与水平面等髙的弧形轻质筐内.己知小球质量为1kg,A、B两点髙度差为2m,斜面BC髙为4m,倾角a=45°,悬挂弧筐的轻绳长为6m,小球可以看成质点,轻质筐的重量忽略不计,弧形轻质筐的大小远小于悬线长度,重力加速度为g=10m/s2.求: