题目内容
3. 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图5所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图5所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断正确的是( )| A. | 两颗卫星的向心加速度大小不相等 | |
| B. | 两颗卫星所受的向心力大小一定相等 | |
| C. | 卫星1由位置A运动到位置B所需的时间可能为$\frac{7πr}{3R}$ $\sqrt{\frac{r}{g}}$ | |
| D. | 如果要使卫星1追上卫星2,一定要使卫星1加速 |
分析 根据万有引力提供向心力得出加速度与轨道半径的关系,从而比较出大小,根据万有引力提供向心力,求出角速度的大小,从而求出卫星1由位置A运动到位置B所需的时间.卫星1在轨道上若加速,所受的万有引力不够提供向心力,做离心运动离开原轨道,不会追上卫星2.
解答 解:A、根据万有引力提供向心力得 G$\frac{Mm}{{r}^{2}}$=ma,得a=$\frac{GM}{{r}^{2}}$.两颗卫星的轨道半径相等,则向心加速度大小相等.故A错误.
B、向心力等于万有引力,而万有引力与卫星的质量有关,则两颗卫星所受的向心力大小不一定相等,则B错误.
C、根据G$\frac{Mm}{{r}^{2}}$=mrω2,GM=gR2,联立解得ω=$\sqrt{\frac{g{R}^{2}}{{r}^{3}}}$,则卫星从位置A运动到位置B的时间可能为 t=$\frac{2π+\frac{π}{3}}{ω}$=$\frac{7πr}{3R}$ $\sqrt{\frac{r}{g}}$.故C正确.
D、如果卫星1加速,万有引力不够提供向心力,做离心运动,离开原轨道,不会追上卫星2.故D错误.
故选:C
点评 解决卫星问题的关键要掌握万有引力提供向心力以及万有引力等于重力这两大理论,并能熟练运用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
13.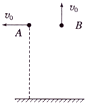 如图,两个相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,忽略空气阻力,下列说法正确的是( )
如图,两个相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,忽略空气阻力,下列说法正确的是( )
 如图,两个相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,忽略空气阻力,下列说法正确的是( )
如图,两个相同的小球A、B,在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出,忽略空气阻力,下列说法正确的是( )| A. | 从开始运动至落地,两小球的运动时间相同 | |
| B. | 从开始运动至落地,重力对两小球做的功相同 | |
| C. | 两小球落地时的速度相同 | |
| D. | 两小球落地时重力的瞬时功率相同 |
14.实验表明,可见光通过三棱镜时各色光的折射率n随着波长λ的变化符合科西经验公式:n=A+$\frac{B}{{λ}^{2}}$+$\frac{C}{{λ}^{4}}$,其中A、B、C是正的常量.太阳光进入三棱镜后发生色散的情形如图所示.则( )
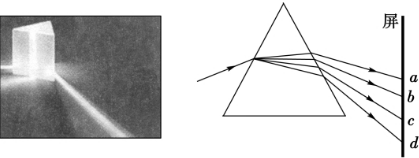

| A. | 屏上d处是紫光 | |
| B. | 屏上d处的光在棱镜中传播速度最大 | |
| C. | 屏上a处是紫光 | |
| D. | 屏上d处的光在棱镜中传播速度最小 | |
| E. | 光经过三棱镜后发生色散原因是不同频率的光在同种介质中折射率不同 |
18.一个物体在三个共点力的作用下做匀速直线运动,则这个三个力的大小可能是( )
| A. | 3N 5N 9N | B. | 5N 10N 10N | ||
| C. | 3N 5N 1N | D. | 20N 7N 10N |
8.关于物理学的研究方法,以下说法错误的是( )


| A. | 开普勒通过大量的数据和观测记录,从而发现了行星运动的三大定律 | |
| B. | 牛顿发现了万有引力定律并用实验方法测出引力常量的数值,从而使万有引力定律有了真正的实用价值 | |
| C. | 在用实验探究加速度、力和质量三者之间关系时,应用了控制变量法 | |
| D. | 如图是三个实验装置,这三个实验都体现了微量放大的思想 |
15. 一轻弹簧的左端固定,右端与一小球相连,小球处于光滑水平面上,现对小球施加一个方向水平向右的力F,使小球从静止开始向右匀加速运动,在小球通过位移为x的过程,弹簧始终未超过弹性限度,对于此过程,下列说法正确的是( )
一轻弹簧的左端固定,右端与一小球相连,小球处于光滑水平面上,现对小球施加一个方向水平向右的力F,使小球从静止开始向右匀加速运动,在小球通过位移为x的过程,弹簧始终未超过弹性限度,对于此过程,下列说法正确的是( )
 一轻弹簧的左端固定,右端与一小球相连,小球处于光滑水平面上,现对小球施加一个方向水平向右的力F,使小球从静止开始向右匀加速运动,在小球通过位移为x的过程,弹簧始终未超过弹性限度,对于此过程,下列说法正确的是( )
一轻弹簧的左端固定,右端与一小球相连,小球处于光滑水平面上,现对小球施加一个方向水平向右的力F,使小球从静止开始向右匀加速运动,在小球通过位移为x的过程,弹簧始终未超过弹性限度,对于此过程,下列说法正确的是( )| A. | F对小球做负功 | |
| B. | F对小球做的功等于弹簧弹性势能的增量 | |
| C. | 小球所受的合外力保持不变 | |
| D. | F的功率保持不变 |
11.已知a金属的逸出功大于b金属的逸出功,用某单色光照射a金属表面,发生了光电效应,现用该单色光照射b金属表面,下列说法正确的是( )
| A. | 不一定能发生光电效应 | |
| B. | 光电子的最大初动能增加 | |
| C. | 单位时间内发射的光电子数目一定增加 | |
| D. | 延长光照时间或增加光照强度才能发生光电效应 |
 如图所示,光滑水平地面上静止放置一质量为M的木板B,B上叠放着一质量为m的木块A,A用绳系在固定的墙上,A、B间动摩擦因数为μ.现用恒力F拉着B向右移动距离S(木板足够长,A始终在B上面),在此过程中,求:
如图所示,光滑水平地面上静止放置一质量为M的木板B,B上叠放着一质量为m的木块A,A用绳系在固定的墙上,A、B间动摩擦因数为μ.现用恒力F拉着B向右移动距离S(木板足够长,A始终在B上面),在此过程中,求: