题目内容

13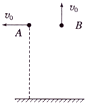．如图，两个相同的小球A、B，在同一高度处以相同大小的初速度v0分别水平抛出和竖直向上抛出，忽略空气阻力，下列说法正确的是（　　）
A．从开始运动至落地，两小球的运动时间相同
B．从开始运动至落地，重力对两小球做的功相同
C．两小球落地时的速度相同
D．两小球落地时重力的瞬时功率相同

分析 根据两球的运动规律，结合运动学公式比较运动的时间，根据下降的高度比较重力做功的大小．根据机械能守恒比较落地的速度，结合瞬时功率的公式比较重力做功的瞬时功率．

解答 解：A、A做平抛运动在竖直方向上做自由落体运动，B做竖直上抛运动，上升到最高点后做自由落体运动，可知两球的运动时间不同，故A错误．
B、两球初末位置的高度差相同，则重力做功相同，故B正确．
C、根据机械能守恒定律知，落地的速度大小相等，方向不同，故C错误．
D、由C选项知，两球落地的速度大小相等，方向不同，根据P=mgvcosθ知，两球落地时重力的瞬时功率不同，故D错误．
故选：B．

点评 在分析功率的时候，一定要注意公式的选择，P=$\frac{W}{t}$只能计算平均功率的大小，而P=Fvcosθ可以计算平均功率也可以是瞬时功率，取决于速度是平均速度还是瞬时速度．

练习册系列答案
相关题目
11．甲、乙两船的质量均为M，它们都静止在平静的湖面上，质量为M的人从甲船跳到乙船上，再从乙船跳回甲船，经过多次跳跃后，最后人停在乙船上．假设水的阻力可忽略，则（　　）
A．甲、乙两船的速度大小之比为1：2B．甲船与乙船（包括人）的动量相同
C．甲船与乙船（包括人）的动量之和为零D．因跳跃次数未知，故无法判断
4．如图所示，一倾角为a的固定斜面下端固定一挡板，一劲度系数为k的轻弹簧下端固定在挡板上．现将一质量为m的小物块从斜面上离弹簧上端距离为s处，由静止释放，已知物块与斜面间的动摩擦因数为μ，物块下滑过程中的最大动能为Ekm，则小物块从释放到运动至最低点的过程中，下列说法中正确的是（　　）
A．μ＜tana
B．物块刚与弹簧接触的瞬间达到最大动能
C．弹簧的最大弹性势能等于整个过程中物块减少的重力势能与摩擦力对物块做功之和
D．若将物块从离弹簧上端2s的斜面处由静止释放，则下滑过程中物块的最大动能小于2Ekm
1．弹簧振子做简谐运动，若某一过程中振子的速率在减小，则此时振子的运动（　　）
A．速度与位移方向一定相反B．加速度与速度方向可能相同
C．回复力一定在增大D．位移可能在减小
8．将一弹簧振子拉到距平衡位置2cm处由静止释放，运动过程中无能量损失，振子第一次到平衡位置所用的时间为0.2s，则振子的频率为1.25Hz，振幅为0.02m．
18．如图所示，两个相同灯泡L1、L2分别与电阻R和自感线圈L串联，接到内阻不计的电源两端，闭合电键S，当电路稳定后，两灯泡均正常发光．已知自感线圈的自感系数很大，阻值与电阻R相同．下列说法正确的是（　　）
A．闭合S到电路稳定前，灯泡L1逐渐变亮
B．闭合S到电路稳定前，灯泡L2逐渐变亮
C．断开S的一段时间内，B点电势比A点电势低
D．断开S的一段时间内，灯泡L2亮一下后逐渐熄灭
5．重核裂变是释放核能的一种核反应，铀核裂变的一个可能的反应${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{55}^{141}$Cs+${\;}_{27}^{93}$Rb+2X，其中${\;}_{92}^{235}$U的质量为235.04392u，${\;}_{55}^{141}$Cs的质量为140.91963u，${\;}_{27}^{93}$Rb的质量为92.92157u，${\;}_{0}^{1}$n的质量是1.000867u，u是原子质量单位，1u相当于931.5MeV的能量，电子电量e=1.6×10-19C．
①核反应中的X是${\;}_{0}^{1}n$；
②核反应中释放的能量是3.01×10-11J（保留三位有效数字）
2．一个质点在水平面内运动的v-t图象如图所示，对应的a-t图象和x-t图象中正确的是（　　）
A．B．C．D．
3．北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能．“北斗”系统中两颗工作卫星1和2均绕地心O做匀速圆周运动，轨道半径均为r，某时刻两颗工作卫星分别位于轨道上的A、B两位置，如图5所示．若卫星均顺时针运行，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．以下判断正确的是（　　）
A．两颗卫星的向心加速度大小不相等
B．两颗卫星所受的向心力大小一定相等
C．卫星1由位置A运动到位置B所需的时间可能为$\frac{7πr}{3R}$ $\sqrt{\frac{r}{g}}$
D．如果要使卫星1追上卫星2，一定要使卫星1加速

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网