题目内容
6. 超市一送水员用双轮小车运送桶装矿泉水.装运完毕,如图所示,在拉运过程中保持图示角度不变,不计桶与小车之间摩擦力的影响.求:(g=10m/s2)
超市一送水员用双轮小车运送桶装矿泉水.装运完毕,如图所示,在拉运过程中保持图示角度不变,不计桶与小车之间摩擦力的影响.求:(g=10m/s2)(1)若送货员以5m/s2的恒定加速度由静止开始水平向右拉动小车时,请问这一过程中,桶对小车两侧轨道的压力大小之比NA:NB.
(2)若送货员水平推拉小车时,桶对小车两侧轨道始终有压力,小车的加速度应满足什么条件?
分析 (1)对桶进行受力分析,建立坐标系,进行正交分解法,沿着x、y方向列式求解;
(2)由(1)中的两个表达式求出两种临界状态即NB=0和NA=0时,对应的加速度即可.
解答 解:(1)对桶进行受力分析,可知:
竖直方向受力平衡,则有:mg=NAcos37°+NBcos53° ①
水平方向,根据牛顿第二定律得:NAsin37°-NBsin53°=ma ②
当a=5m/s2时,由①②解得:NA:NB=1:2
再根据牛顿第三定律,桶对小车两侧轨道的压力大小之比为1:2;
(2)由根据mg=NAcos37°+NBcos53°
NAsin37°-NBsin53°=ma
可知:当NB=0时,有向右的最大加速度${a}_{1}=gtan37°=7.5m/{s}^{2}$
当NA=0时,有向左的最大加速度a2=gtan53°=13.3m/s2
所以,要使桶对小车两侧轨道的始终有压力,小车向左的加速度要小于13.3 m/s2,向右的加速度要小于7.5 m/s2.
答:(1)桶对小车两侧轨道的压力大小之比为1:2.
(2)小车向左的加速度小于13.3 m/s2,向右的加速度小于7.5 m/s2.
点评 考查物体平衡条件和牛顿第二定律,规范作图受力分析后,根据情况采用合成法或正交分解法,进行列式求解.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
11.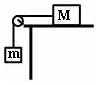 如图所示,已知M>m,不计滑轮及绳子的质量,物体M和m恰好做匀速运动,若将M与m 互换,M、m与桌面的动摩因数相同,则( )
如图所示,已知M>m,不计滑轮及绳子的质量,物体M和m恰好做匀速运动,若将M与m 互换,M、m与桌面的动摩因数相同,则( )
 如图所示,已知M>m,不计滑轮及绳子的质量,物体M和m恰好做匀速运动,若将M与m 互换,M、m与桌面的动摩因数相同,则( )
如图所示,已知M>m,不计滑轮及绳子的质量,物体M和m恰好做匀速运动,若将M与m 互换,M、m与桌面的动摩因数相同,则( )| A. | 物体M与m仍做匀速运动 | |
| B. | 物体M与m做加速运动,加速度a=$\frac{(M+m)g}{M}$ | |
| C. | 物体M与m做加速运动,加速度a=$\frac{(M-m)g}{M}$ | |
| D. | 绳子中张力不变 |
16.下列说法正确的是( )
| A. | 位移是描述物体位置变化大小的物理量 | |
| B. | 速度是物体运动的路程与所用时间的比值 | |
| C. | 在生活中能找到质点这样的物体 | |
| D. | 加速度是描述速度变化快慢及方向的物理量 |
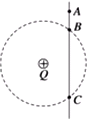 如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时的速度大小为$\sqrt{7gh}$.求:
如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时的速度大小为$\sqrt{7gh}$.求:
 如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉N瞬间,小球加速度的大小为12m/s2.若不拔去销钉N而拔去M销钉瞬间,小球的加速度可能是?(取g=10m/s2)
如图所示,竖直光滑杆上套有一个小球和两根弹簧,两弹簧的一端各与小球相连,另一端分别用销钉M、N固定于杆上,小球处于静止状态.设拔去销钉N瞬间,小球加速度的大小为12m/s2.若不拔去销钉N而拔去M销钉瞬间,小球的加速度可能是?(取g=10m/s2)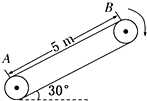 如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=5kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2)
如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=5kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2) 如图所示,斜面AB倾角为30°,底端A点与斜面上B点相距10m,甲、乙两物体大小不计,与斜面间的动摩擦因数为$\frac{\sqrt{3}}{2}$,某时刻甲从A点沿斜面以v1=10m/s的初速度滑向B,同时乙物体从B点以v2=7.25m/s的初速度滑向A,(g=10m/s2 最大静摩擦力等于滑动摩擦力)求:
如图所示,斜面AB倾角为30°,底端A点与斜面上B点相距10m,甲、乙两物体大小不计,与斜面间的动摩擦因数为$\frac{\sqrt{3}}{2}$,某时刻甲从A点沿斜面以v1=10m/s的初速度滑向B,同时乙物体从B点以v2=7.25m/s的初速度滑向A,(g=10m/s2 最大静摩擦力等于滑动摩擦力)求: