题目内容
2. 如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.
如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.
分析 b、c、d三点是同轴传动,角速度相等;a、c点是同缘传动边缘点,线速度相等;结合公式a=ω2r和v=ωr分析.
解答 解:①a、c点是同缘传动边缘点,线速度相等,va:vc=1:1;
②根据v=ωr,ωa:ωc=rc:ra=2:1,b、c、d两个点是同轴传动,角速度相等,ωa:ωb=2:1;
故答案为:1:1; 2:1.
点评 本题关键是明确同缘传动边缘点线速度相等,同轴传动角速度相等,然后根据公式a=ω2r和v=ωr并采用控制变量法分析.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
12.关于曲线运动,下列说法中正确的是( )
| A. | 恒力作用下的物体的运动不可能是曲线运动 | |
| B. | 变力作用下的物体的运动一定是曲线运动 | |
| C. | 匀速圆周运动是非匀变速运动 | |
| D. | 平抛是匀变速运动 |
17.如图所示是光的双缝干涉的示意图,下列说法中正确的是( )


| A. | 单缝S的作用是为了增加光的强度 | |
| B. | 当S1、S2发出两列光波到P点的路程差为光的波长λ的0.5倍时,产生第二暗条纹 | |
| C. | 双缝S1、S2的作用是为了产生两个频率相同的线状光源 | |
| D. | 当S1、S2发出的两列光波到P点的路程差为波长λ时,产生中央亮条纹 |
12. 三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB>MC,则对于三个卫星,正确的是( )
三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB>MC,则对于三个卫星,正确的是( )
 三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB>MC,则对于三个卫星,正确的是( )
三颗人造地球卫星A、B、C绕地球作匀速圆周运动,如图所示,已知MA=MB>MC,则对于三个卫星,正确的是( )| A. | 运行线速度关系为vA>vB=vC | |
| B. | 运行周期关系为 TA=TB=TC | |
| C. | 向心力大小关系为FA>FB>FC | |
| D. | 自己半径与周期关系为 $\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求: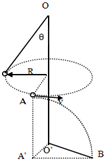 如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求:
如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求: